如图,半径为R的光滑半圆形轨道ABC在竖直平面内,与水平轨道CD相切于C 点,D端有一被锁定的轻质压缩弹簧,弹簧左端连接在固定的挡板上,弹簧右端Q到C点的距离为2R。质量为m的滑块(视为质点)从轨道上的P点由静止滑下,刚好能运动到Q点,并能触发弹簧解除锁定,然后滑块被弹回,且刚好能通过圆轨道的最高点A。已知∠POC=60°,求:
⑴滑块第一次滑至圆形轨道最低点C时对轨道压力;
⑵滑块与水平轨道间的动摩擦因数μ;
⑶弹簧被锁定时具有的弹性势能。
如图所示,在游乐节目中,选手需要借助悬挂在高处的绳飞越对面的高台上. 一质量m=60kg的选手脚穿轮滑鞋以v0=7m/s的水平速度抓住竖直的绳开始摆动,选手可看作质点,这时,绳子的悬挂点到选手的距离L=6m.当绳摆到与竖直方向夹角θ=37°时,选手放开绳子。不考虑空气阻力和绳的质量.取重力加速度g="10m/s2," sin370=0.6,cos370=0.8.求: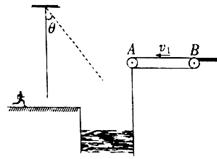
(1)选手放开绳子时的速度大小;
(2)选手放开绳子后继续运动到最高点时,刚好可以站到水平传送带A点, 传送带始终以v1=3m/s的速度匀速向左运动,传送带的另一端B点就是终点,且SAB=3.75m.若选手在传送带上不提供动力自由滑行,受到的摩擦阻力为自重的0.2倍,通过计算说明该选手是否能顺利冲过终点B,并求出选手在传送带上滑行过程中因摩擦而产生的热量Q。
某农田自动灌溉的喷射装置的截面图如图所示,它主要由水泵、竖直的细输水管道和喷头组成,喷头的喷嘴(长度可忽略不计)离地面的高度为h。水泵启动后,水从水池通过输水管道压到喷嘴并沿水平方向喷出,在地面上的落点与输水管道中心的水平距离为R,此时喷嘴每秒喷出水的质量为m0 ,整个供水系统的效率恒为η。忽略水池中水泵与地面的高度差,不计水进入水泵时的速度以及空气阻力,重力加速度为g。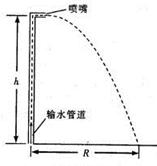
(1)求水从喷嘴喷出时的速度v;
(2)求水泵的功率p;
(3)若要浇灌离输水管道中心R1处的蔬菜,求此时喷嘴每秒钟喷出水
的质量m1和水泵的功率p1。
小李同学乘坐杭温线“和谐号”动车组,发现车厢内有速率显示屏。当动车组在平直轨道上经历匀加速、匀速与再次匀加速运行期间,他记录了不同时刻的速率,部分数据列于表格中。已知动车组的总质量M=2.0×105kg,假设动车组运动时受到的阻力是其重力的0.1倍,取g=10m/s2。在小李同学记录动车组速率这段时间内,求:
| t/s |
v/m·s-1 |
| 0 |
30 |
| 100 |
40 |
| 300 |
50 |
| 400 |
50 |
| 500 |
60 |
| 550 |
70 |
| 600 |
80 |
(1)动车组的加速度值;
(2)动车组牵引力的最大值;
(3)动车组位移的大小。
如图所示,在倾角θ=30°的斜面上有一块竖直放置的挡板,在挡板和斜面之间放有一个光滑圆球,当系统静止时档板上的压力传感器显示压力为20N,试求:
(1)球对斜面的压力和圆球的重力。
(2)要让挡板压力为零,整个装置在水平方向上将怎样运动?
如图所示,水平平台的右端安装有轻质滑轮,质量为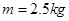 的物块A放在与滑轮相距
的物块A放在与滑轮相距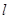 的平台上,现有一轻绳跨过定滑轮,左端与物块连接,右端挂质量为
的平台上,现有一轻绳跨过定滑轮,左端与物块连接,右端挂质量为 的小球B,绳拉直时用手托住小球使其在距地面h高处静止,绳与滑轮间的摩擦不计,重力加速度为
的小球B,绳拉直时用手托住小球使其在距地面h高处静止,绳与滑轮间的摩擦不计,重力加速度为 (
( 取
取 )。设最大静摩擦力等于滑动摩擦力.
)。设最大静摩擦力等于滑动摩擦力.
(1)某探究小组欲用上述装置测量物块与平台间的动摩擦因数。放开小球,系统运动,该小组对小球匀加速下落过程拍得同一底片上多次曝光的照片如图所示,拍摄时每隔1s曝光一次,若小球直径为20cm,求物块A与平台间的动摩擦因数 ;
;
(2)设小球着地后立即停止运动,已知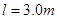 ,要使物块A不撞到定滑轮,求小球下落的最大高度h?(假设小球距地面足够高)
,要使物块A不撞到定滑轮,求小球下落的最大高度h?(假设小球距地面足够高)