如图1所示,宽度为d的竖直狭长区域内(边界为L1、L2),存在垂直纸面向里的匀强磁场和竖直方向上的周期性变化的电场(如图2所示),电场强度的大小为E0,E0>0表示电场方向竖直向上.t=0时,一带正电、质量为m的微粒从左边界上的N1点以水平速度v射入该区域,沿直线运动到Q点后,做一次完整的圆周运动,再沿直线运动到右边界上的N2点.Q为线段N1N2的中点,重力加速度为g.上述d、E0、m、v、g为已知量.
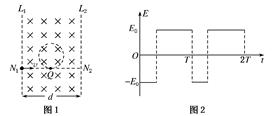
(1)求微粒所带电荷量q和磁感应强度B的大小;
(2)求电场变化的周期T;
(3)改变宽度d,使微粒仍能按上述运动过程通过相应宽度的区域,求T的最小值.
湖南省电视台“智勇大冲关”游乐节目中,选手需要借助悬挂在高处的绳飞越到水面的浮台上,小明和小阳观看后对此进行了讨论。如图(13)所示,他们将选手简化为质量m=60kg的质点,选手抓住绳子末端由静止开始摆动,此时绳与竖直方向夹角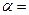 53°,绳长l=2m的悬挂点O距水面的高度为H=3m。不考虑空气阻力和绳的质量,浮台露出水面的高度不计,水足够深。取g=10m/s2(sin53o=0.8,cos53o=0.6)。求:
53°,绳长l=2m的悬挂点O距水面的高度为H=3m。不考虑空气阻力和绳的质量,浮台露出水面的高度不计,水足够深。取g=10m/s2(sin53o=0.8,cos53o=0.6)。求:
(1)选手摆到最低点时对绳拉力的大小F;
(2)选手摆到右边最高点时松手,设水对选手的平均浮力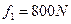 ,平均阻力
,平均阻力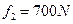 ,求选手落入水中的深度
,求选手落入水中的深度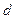 ;
;
(3)若要求选手摆到最低点时松手,且运动到浮台处离岸水平距离最大,则选手实际的摆线长度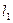 应为多少?
应为多少?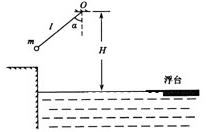
近年来,我国汽车工业发展迅速,自主品牌纷纷崛起,如奇瑞、吉利、比亚迪等,不仅产销红火,甚至出口国外. 比亚迪公司本来是做电池起家的,在电池制造方面独具优势,该公司生产的“比亚迪铁动力F3”性能优良,这种汽车利用技术独特的充电电池——“铁电池”提供能量,充足电可行驶400公里,且在15分钟内即可充电至满容量的80%,因此使用比较方便,且对环境没有污染.设该车质量m=1.5t,额定功率P=60kW,最高时速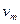 =144km/h,g=10
=144km/h,g=10 . 求:
. 求:
(1)该汽车在水平路面上以最高时速行驶时所受的阻力是多少?
(2)设行驶中汽车所受阻力与速度大小无关,该车以额定功率P行驶,当速度增大到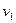 =72km/h时的瞬时加速度
=72km/h时的瞬时加速度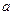 是多大?
是多大?
如图所示,第四象限内有互相正交的匀强电场E与匀强磁场B1, E的大小为0.5×103V/m, B1大小为0.5T;第一象限的某个矩形区域内,有方向垂直纸面向里的匀强磁场B2,磁场的下边界与x轴重合.一质量m=1×10-14kg、电荷量q=1×10-10C的带正电微粒以某一速度v沿与y轴正方向60°角从M点沿直线运动,经P点即进入处于第一象限内的磁场B2区域.一段时间后,小球经过y轴上的N点并与y轴正方向成60°角的方向飞出。M点的坐标为(0,-10),N点的坐标为(0,30),不计粒子重力, g取10m/s2.
(1)请分析判断匀强电场E1的方向并求出微粒的运动速度v;
(2)匀强磁场B2的大小为多大?;
(3) B2磁场区域的最小面积为多少?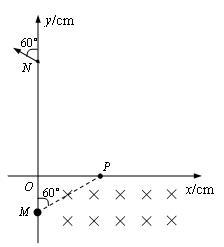
如图24-1所示,R1=R2=R3=R4=R,电键S闭合时,间距为d的平行板电容器C 的正中间有一质量为m,带电量为q的小球恰好处于静止状态;电键S断开时,小球向电容器一个极板运动并发生碰撞,碰撞后小球带上与极板同种性质的电荷。设碰撞过程中没有机械能损失,小球反弹后恰好能运动到电容器另一极板。若不计电源内阻,求:
(1)电源的电动势;
(2)小球与极板碰撞后的带电量。
如图2-1所示,轻质长绳水平地跨在相距为2L的两个小定滑轮A、B上,质量为m的物块悬挂在绳上O点,O与A、B两滑轮的距离相等。在轻绳两端C、D分别施加竖直向下的恒力F=mg。先托住物块,使绳处于水平拉直状态,由静止释放物块,在物块下落过程中,保持C、D两端的拉力F不变。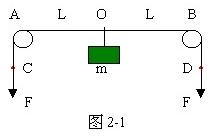
(1)当物块下落距离h为多大时,物块的加速度为零?
(2)在物块下落上述距离的过程中,克服C端恒力F做功W为多少?
(3)求物块下落过程中的最大速度Vm和最大距离H?