某大学校园内一商店，销售一种进价为每件20元的台灯．销售过程中发现，每月销售量y（件）与销售单价x（元）之间的关系可近似的看作一次函数：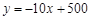
．
（1）设此商店每月获得利润为w（元），求w与x的函数关系式，并求出w的最大值；
（2）如果此商店想要每月获得2000元的利润，那么销售单价应定为多少元？
（3）根据物价部门规定，这种台灯的销售单价不得高于32元，如果此商店想要每月获得的利润不低于2000元，那么商店每月的成本最少需要多少元？
有一块直角三角形纸片，两直角边AC=6cm，BC=8cm。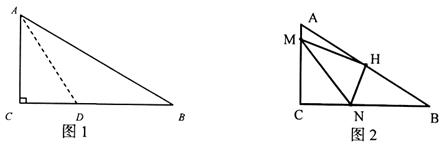
如图1，现将纸片沿直线AD折叠，使直角边AC落在斜边AB上，且与AB重合，则CD=。
如图2，若将直角
C沿MN折叠，使点C落在AB中点H上，点M、N分别在AC、BC上，则
、
与
之间有怎样的数量关系？并证明你的结论。
在下面所给的图形中，若连接BC，则四边形ABCD是矩形，四边形CBEF是平行四边形。用铅笔和三角板画图：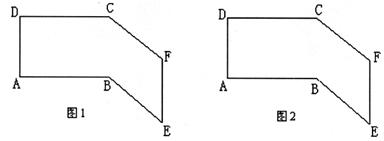
在图1中画出两条线段，将整个图形分成面积相等的两个部分（不写画法）；
在图2中画出一条线段，还能够将整个图形分成面积相等的两个部分，并写出画法的主要步骤。
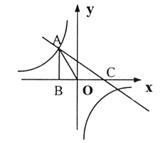
已知反比例函数
的图象过点A（
），过点A作AB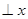
轴于点B，且
AOB的面积为
。
求
和
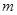的值；若一次函数
的图象经过点A，并且与
轴相交于点C，求
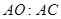的值
甲乙二人同时从张庄出发，步行15千米到李庄，甲比乙每小时多走1千米，结果比乙早到半小时。问二人每小时各走几千米？
在2ABCD中，对角线BD、AC相交于点O，BE=DF，过点O作线段GH交AD于点G，交BC于点H，顺次连接EH、HF、FG、GE，求证：四边形EHFG是平行四边形。