阅读并解答下列问题：我们熟悉两个乘法公式：①（
+b）2=2+2b+b2;②(-b)2=2-2b+b2.现将这两个公式变形，可得到一个新的公式③：b=(
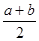)2-(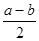
)2, 这个公式形似平方差公式，我们不妨称之为广义的平立差公式。灵活、恰当地运用公式③将会使一些数学问题迎刃而解。
例如：因式分解：（b-1）2+(+b-2)( +b-2b)
解：原式=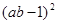
+
-
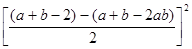
=(b-1)2+(+b-b-1)2-(b-1)2=(-1)(b-1)2=（-1）2(b-1)2你能利用公式（或其他方法）解决下列问题吗？
已知各实数，b，c满足b=c2+9且=6-b，求证：="b"
如图，在Rt△ABC中，∠ACB＝90°，以AC为直径的⊙O与AB边交于点D，点E是边BC的中点．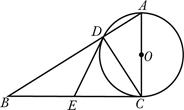
（1）求证：BC 2＝BD•BA；（2）判断DE与⊙O位置关系，并说明理由.
已知：如图，AB是⊙O的直径，CD是⊙O的弦，且AB⊥CD，垂足为E．
（1）求证：∠CDB＝∠A；
（2）若BD＝5，AD＝12，求CD的长．
小丽和小静两人玩“剪刀、石头、布”的游戏，游戏规则为：剪刀胜布，布胜石头，石头胜剪刀．
（1）请用列表法或树状图表示出所有可能出现的游戏结果；
（2）求小丽胜出的概率．
如图，小明与同学合作利用太阳光线测量旗杆的高度，身高1.6 m的小明落在地面上的影长为BC＝2.4m．
（1）请你在图中画出旗杆在同一时刻阳光照射下落在地面上的影子EG；
（2）若小明测得此刻旗杆落在地面的影长EG＝16 m，请求出旗杆DE的高度．
已知：二次函数
．
（1）求出该二次函数图象的对称轴和顶点坐标；
（2）求出该抛物线与x轴的交点坐标；
（3）当x取何值时，y＜0.