已知：如图，抛物线y=ax2-2ax+c(a≠0)与y轴交于点C（0，4），与x轴交于点A、B，点A的坐标为（4，0）。 求该抛物线的解析式； 点Q是线段AB上的动点，过点Q作QE∥AC，交BC于点E，连接CQ。当△CQE的面积最大时，求点Q的坐标； 若平行于x轴的动直线l与该抛物线交于点P，与直线AC交于点F，点D的坐标为（2，0）。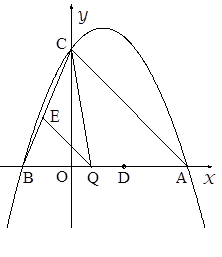
问：是否存在这样的直线l，使得△ODF是等腰三角形？若存在，请求出点P的坐标若不存在，请说明理由。
（本小题满分8分）小敏和小兰都想当节目主持人，但现在名额只有1个，为了能够选出1人参加，小丽想了一个办法：在三张卡片上分别写着3、-4、4，放入盒子里搅匀，随机抽取2张，若两张卡片上的数字之和为0，小敏当主持人，否则小兰当主持人，你认为这个游戏公平吗？用数据说明你的观点．
（本小题满分7分）
解不等式组
，并将它的解集在数轴上标出来．
（本小题满分7分，其中（1）小题3分，（2）小题4分）
解下列二元一次方程组：
（1）
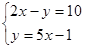
（2）
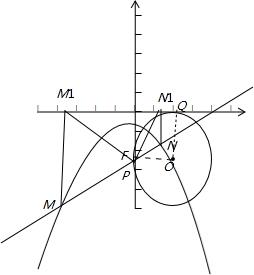
已知二次函数y=ax2+bx+c的图象的顶点坐标为 (0，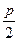
)，且 ac=
．
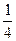（1）若该函数的图象经过点（-1，-1）．
①求使y＜0成立的x的取值范围．
②若圆心在该函数的图象上的圆与x轴、y轴都相切，求圆心的坐标．
（2）经过A（0，p）的直线与该函数的图象相交于M，N两点，过M，N作x轴的垂线，垂足分别为M1，N1，设△MAM1，△A
M1N1，△ANN1的面积分别为s1，s2，s3，是否存在m，使得对任意实数p≠0都有s22=ms1s3成立，若存在，求出m的值，若不存在，请说明理由．