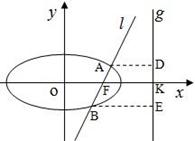
如图,已知直线l:x=my+1过椭圆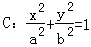 的右焦点F,抛物线:
的右焦点F,抛物线: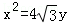 的焦点为椭圆C的上顶点,且直线l交椭圆C于A、B两点,点A、F、B在直线g:x=4上的射影依次为点D、K、E.(1)椭圆C的方程;(2)直线l交y轴于点M,且
的焦点为椭圆C的上顶点,且直线l交椭圆C于A、B两点,点A、F、B在直线g:x=4上的射影依次为点D、K、E.(1)椭圆C的方程;(2)直线l交y轴于点M,且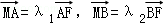 ,当m变化时,探求λ1+λ2的值是否为定值?若是,求出λ1+λ2的值,否则,说明理由;(3)接AE、BD,试证明当m变化时,直线AE与BD相交于定点
,当m变化时,探求λ1+λ2的值是否为定值?若是,求出λ1+λ2的值,否则,说明理由;(3)接AE、BD,试证明当m变化时,直线AE与BD相交于定点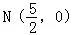 .
.
在直角坐标系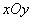 中,以
中,以 为圆心的圆与直线
为圆心的圆与直线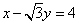 相切.
相切.
(1)求圆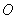 的方程;(2)圆
的方程;(2)圆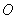 与
与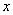 轴相交于
轴相交于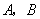 两点,圆内的动点
两点,圆内的动点 使
使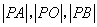 成等比数列,求
成等比数列,求 的取值范围
的取值范围
已知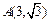 ,O是原点,点P(x, y)的坐标满足
,O是原点,点P(x, y)的坐标满足

(1)求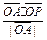 的最大值.;(2)求
的最大值.;(2)求 的取值范围.
的取值范围.
如图所示,已知直线 与
与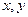 轴的正半轴分别交于
轴的正半轴分别交于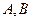 两点,直线
两点,直线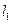 和
和 分别交于
分别交于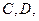 且平分△
且平分△ 的面积,求
的面积,求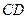 的最小值.
的最小值.
如图所示,F1、F2分别为椭圆C: 的左、右两个焦点,A、B为两个顶点,
的左、右两个焦点,A、B为两个顶点,
已知椭圆C上的点 到F1、F2两点的距离之和为4.
到F1、F2两点的距离之和为4.
(Ⅰ)求椭圆C的方程和焦点坐标;
(Ⅱ)过椭圆C的焦点F2作AB的平行线交椭圆于P、Q两点,求△F1PQ的面积.
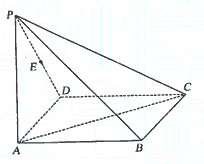
如图,在四棱锥P—ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,AB= ,BC=1,PA=2,E为PD的中点.
,BC=1,PA=2,E为PD的中点.
(Ⅰ)求直线AC与PB所成角的余弦值;
(Ⅱ)在侧面PAB内找一点N,使NE⊥面PAC,并求出N点到AB和AP的距离.