如图,在四棱锥P—ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,AB= ,BC=1,PA=2,E为PD的中点.
,BC=1,PA=2,E为PD的中点.
(Ⅰ)求直线AC与PB所成角的余弦值;
(Ⅱ)在侧面PAB内找一点N,使NE⊥面PAC,并求出N点到AB和AP的距离. 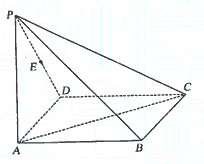
某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[20,25),需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
|
最高气温 |
|
|
|
|
|
|
|
天数 |
2 |
16 |
36 |
25 |
7 |
4 |
以最高气温位于各区间的频率代替最高气温位于该区间的概率。
(1)求六月份这种酸奶一天的需求量不超过300瓶的概率;
(2)设六月份一天销售这种酸奶的利润为 (单位:元),当六月份这种酸奶一天的进货量为450瓶时,写出 的所有可能值,并估计 大于零的概率.
设数列
满足
.
(1)求 的通项公式;
(2)求数列
的前
 项和.
项和.
在平面直角坐标系xOy中,设点集
,
令 .从集合 M n中任取两个不同的点,用随机变量 X表示它们之间的距离.
(1)当 n=1时,求 X的概率分布;
(2)对给定的正整数 n( n≥3),求概率 P( X≤ n)(用 n表示).
设
.已知
.
(1)求 n的值;
(2)设 ,其中 ,求 的值.
设
,解不等式
.