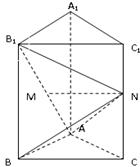
如图,在正三棱柱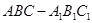 中,
中,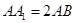 ,
, 是
是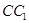 的中点,
的中点, 是线段
是线段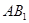 上的动点(与端点不重合),且
上的动点(与端点不重合),且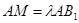 .
.
(1)若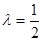 ,求证:
,求证: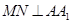 ;
;
(2)若直线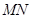 与平面
与平面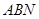 所成角的大小为
所成角的大小为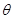 ,求
,求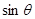 的最大值.
的最大值.
在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2AB=2.
(Ⅰ)若F为PC的中点,求证PC⊥平面AEF;
(Ⅱ)求四棱锥P-ABCD的体积V.
在△ABC中, 分别是角A,B,C的对边,
分别是角A,B,C的对边, ,
, .
.
(Ⅰ)求角 的值;
的值;
(Ⅱ)若 ,求△ABC面积.
,求△ABC面积.
某电视台综艺频道组织的闯关游戏,游戏规定前两关至少过一关才有资格闯第三关,闯关者闯第一关成功得3分,闯第二关成功得3分,闯第三关成功得4分.现有一位参加游戏者单独面第一关、第二关、第三关成功的概率分别为 ,
, ,
, ,记该参加者闯三关所得总分为ζ.
,记该参加者闯三关所得总分为ζ.
(1)求该参加者有资格闯第三关的概率;
(2)求ζ的分布列和数学期望.
如图,在边长为 的正方体
的正方体 中,
中, 、
、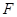 分别是
分别是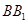 、
、 的中点,试用向量的方法:
的中点,试用向量的方法: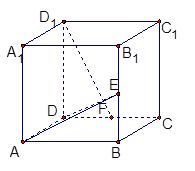
 求证:
求证: 平面
平面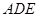 ;
;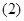 求
求 与平面
与平面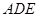 所成的角的余弦值.
所成的角的余弦值.
已知直线 在极坐标系中的方程为
在极坐标系中的方程为 ,圆C在极坐标系中的方程为
,圆C在极坐标系中的方程为 ,求圆C被直线
,求圆C被直线 截得的弦长.
截得的弦长.