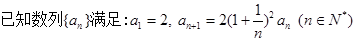
(1)求证:  是等比数列,并求出
是等比数列,并求出 的通项公式;
的通项公式;
(2) ,
, ,
, 
(本小题满分12分)已知A={xㄧx2-3x-4<0 },B={xㄧx2-4x+3>0 },
求A∩B
比较下列各组中两个代数式的大小:
⑴x2+3与3x ;
⑵已知a,b为正数,且a≠b,比较a3 +b3与a2b+ab2
(本小题满分10分)解不等式: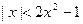 .
.
如图,圆柱 内有一个三棱柱
内有一个三棱柱 ,三棱柱的底面为圆柱
,三棱柱的底面为圆柱
底面的内接三角形,且 是圆
是圆 的直径。
的直径。
(I)证明:平面 平面
平面 ;
;
(II)设 ,在圆
,在圆 柱
柱 内随机选取一点,记该点取自三棱柱
内随机选取一点,记该点取自三棱柱 内的概率为
内的概率为 。
。
(i)当点 在圆周上运动时,求
在圆周上运动时,求 的最大值;
的最大值;
(ii)如果平面 与平面
与平面 所成的角为
所成的角为 。当
。当 取最大值时,求
取最大值时,求
 的值。
的值。
如图,四棱锥P—ABCD的底面是A B=2,BC=
B=2,BC= 的矩形,侧面PAB
的矩形,侧面PAB
是等边三角形,且侧面PAB⊥底面ABCD
(I)证明:侧面PAB⊥侧面PBC;
(II)求侧棱PC与底面ABCD所成的角;
(III)求直线AB与平面PCD的距离.