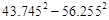两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,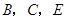 在同一条直线上,连结
在同一条直线上,连结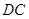 .
.
(1)请找出图2中的全等三角形,并给予证明(说明:结论中不得含有未标识的字母);
(2)证明: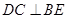 .
.
平面直角坐标系xOy中,抛物线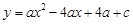 与x轴交于点A、点B,与y轴的正半轴交于点C,点 A的坐标为(1,0),OB=OC,抛物线的顶点为D.
与x轴交于点A、点B,与y轴的正半轴交于点C,点 A的坐标为(1,0),OB=OC,抛物线的顶点为D.
(1)求此抛物线的解析式;
(2)若此抛物线的对称轴上的点P满足∠APB=∠ACB,求点P的坐标;
(3)在(1)的条件下,对于实数c、d,我们可用min{ c,d }表示c、d两数中较小的数,如min{3,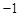 }=
}=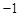 .若关于x的函数y = min{
.若关于x的函数y = min{ ,
,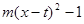
 }的图象关于直线
}的图象关于直线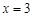 对称,试讨论其与动直线
对称,试讨论其与动直线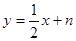 交点的个数。
交点的个数。
在矩形ABCD中,点P在AD上,AB=2,AP=1,将三角板的直角顶点放在点P处,三角板的两直角边分别能与AB、BC边相交于点E、F,连接EF.
(1)如图,当点E与点B重合时,点F恰好与点C重合,求此时PC的长;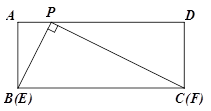
(2)将三角板从(1)中的位置开始,绕点P顺时针旋转,当点E与点A重合时停止,在这个过程中,请你观察、探究并解答: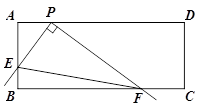
①∠PEF的大小是否发生变化?请说明理由;
②直接写出从开始到停止,线段EF的中点所经过的路线长.
2009年4月7日,国务院公布了《医药卫生体制改革近期重点实施方案(2009—2011)》。某市政府决定2009年投入6000万元用于改善医疗卫生服务,比2008年增加了1250万元,投入资金的服务对象包括“需方”(患者等)和“供方”(医疗卫生机构等),预计2009年投入“需方”的资金将比2008年提高了30%,投入“供方”的资金将比2008年提高20%。
(1)该市政府2008年投入改善医疗卫生服务的资金是多少万元?
(2)该市政府2009年投入“需方”和“供方”的资金分别是多少万元?
(3)该市政府预计2011年将7260万元投入改善医疗卫生服务,若从2009年—2011年每年的资金投入按相同的增长率递增,求2009—2011年的年增长率。
“十·一”黄金周期间,南京市中山陵风景区在7天假期中每天旅游的人数变化如表(正数表示比前一天多的人数,负数表示比前一天少的人数):
| 日期 |
1日 |
2日 |
3日 |
4日 |
5日 |
6日 |
7日 |
| 人数变化(单位:万人) |
1.6 |
1 |
0.4 |
-1 |
-0.8 |
0.4 |
-1.6 |
(1)根据给出的数据,请判断这七天中是否存在着这样的两天,使这两天内景区的游客人数相同?如果存在,是哪两天?如果不存在,请你找出游客人数最接近的两天,并计算它们相差多少万人?
(2)若9月30日该景区的游客人数为2万人,景区门票原价80元/人,黄金周的前三天(10月1日-10月3日)为控制景区人数,将门票单价上浮25%,第四天(10月4日)起票价恢复到原价,试问:这7天的景区门票总收入是多少(精确到百万元)?
探索与应用
【列 式】
在边长为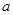 的正方形中挖去一个边长为
的正方形中挖去一个边长为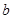 的小正方形(
的小正方形(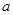 >
>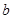 )(如图甲),把余下的部分剪拼成一个长方形(如图乙),
)(如图甲),把余下的部分剪拼成一个长方形(如图乙),
试用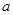 、
、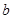 列式:
列式:
图甲中阴影部分的面积为,
图乙中阴影部分的面积为。
【填 表】
根据表格所给的a、b的值,计算 与
与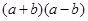 的值,并将计算结果填入表中
的值,并将计算结果填入表中
| a |
2 |
0 |
-2 |
… |
| b |
-3 |
 |
1 |
… |
 |
… |
|||
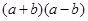 |
… |
【猜 想】
结合(1)、(2)中获得的经验,你能得出结论 :
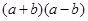 (填“>”,“=”或“<”)
(填“>”,“=”或“<”)
【应 用】
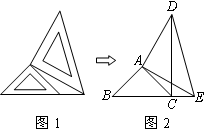
请你用你发现的结论进行简便运算: