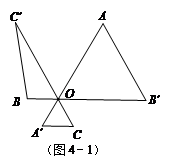如图，A、B表示两个村庄，直线X表示高速公路，已知AB=50km,A、B到直线X的距离分别为10km和40km,要在高速公路旁修建一出口P.小民设计了两种方案，图（1）是方案一的示意图(AP与直线X垂直，垂足为P),P到A、B的距离之和S1=PA+PB； 图（2）是方案二的示意图(点A关于直线X的对称点是A'，连接BA'交直线X于点P),P到A、B的距离之和S2=PA+PB. 
(1)求S1 、S2 ,并比较它们的大小.
(2)请你说明S2=PA+PB的值为最小.
(3)拟建的另一高速公路Y与高速公路X垂直，建立如图所示的直角坐标系，B到直线Y的距离为30km,请你在X旁和Y旁各修建一出口P、Q,使P、A、B、Q 组成的四边形的周长最小.并求出这个最小值.
对于任意的有理数a，b，c，d，我们规定
如： 
，根据这一规定，解答下列问题：化简
若x，y同时满足
=5，
，求x+y的值
判断下列事件哪些是必然事件，哪些是不确定事件，哪些是不可能事件？
事件1：三条边对应相等的两个三角形全等
事件2：三个角对应相等的两个三角形全等
事件3：有两边和其中一边上的中线对应相等的两个三角形全等
事件4：有两边和其中一边的对角对应相等的两个三角形全等
事件5：有两角和其中一角的对边对应相等的两个三角形全等对于事件4，现在我们通过画图来说明。例如，已知∠α和线段a，b.用直尺和圆规作△ABC，使得∠C=∠α，AC=b,AB=a
计算
解决问题：如图，已知正方形ABCD，点E是边AB上一动点，点F在AB边或其延长线上，点G在边AD上．连结ED，FG，交点为H．如图1，若AE=BF=GD，请直接写出∠EHF=▲°；
如图2，若EF =
CD，GD=AE，设∠EHF=α．请判断当点E在AB上运动时， ∠EHF的大小是否发生变化？若发生变化，请说明理由；若不发生变化，请求出tanα．
在图形的全等变换中，有旋转变换，翻折（轴对称）变换和平移变换．一次数学活动课上，老师组织大家利用矩形进行图形变换的探究活动．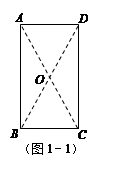
第一小组的同学发现，在如图1－1的矩形ABCD中，AC、BD相交于点O，Rt△ADC可以由Rt△ABC经过一种变换得到，请你写出这种变换的过程是▲．
第二小组同学将矩形纸片ABCD按如下顺序进行操作：对折、展平，得折痕EF（如图2－1）；再沿GC折叠，使点B落在EF上的点B'处（如图2－2），这样能得到∠B'GC的大小，你知道∠B'GC的大小是多少吗？请写出求解过程．
第三小组的同学，在一个矩形纸片上按照图3－1的方式剪下△ABC，其中BA＝BC，将△ABC沿着直线AC的方向依次进行平移变换，每次均移动AC的长度，得到了△CDE、△EFG和△GHI，如图3－2．已知AH＝AI，AC长为a，现以AD、AF和AH为三边构成一个新三角形，已知这个新三角形面积小于15，请你帮助该小组求出a可能的最大整数值．
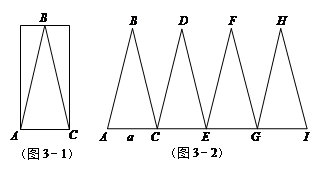
探究活动结束后，老师给大家留下了一道探究题:
如图4－1，已知AA'＝BB'＝CC'＝2，∠AOB'＝∠BOC'＝∠COA'＝60°，请利用图形变换探究S△AOB'＋S△BOC'＋S△COA'与的大小关系．