水果商李老板在高州市收购有香蕉120吨,在海口市收购有香蕉60吨,现要销往北京100吨,沈阳80吨(全部用汽车运输).已知从高州运一吨香蕉到北京和沈阳分别需800元和1000元;从海口运一吨香蕉到北京和沈阳分别需1000元和1300元.
(1)设从海口运往北京x吨,求总运费y(元)关于x(吨)的函数关系式;
(2)李老板计划用17万元开支运费,够用吗?
(3)若每辆车装10吨,且不能浪费车力.李老板要把总运费控制在不超过17.5万元,有多少种调运方案可实现?
(4)请根据前面的要求画出这一函数的图象.
如图,已知点B、C、D在同一条直线上,△ABC和△ECD均是等边三角形.BE与AC交于点H,AD与CE交于点G.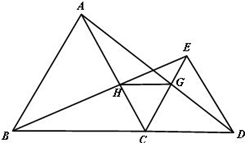
(1)求证:△BCE≌△ACD;
(2)判断GH与BD的位置关系,并证明.
如图,点B在线段AC上,点D,E在AC同侧,∠A=∠C=90°,BD⊥BE,AD=BC.
求证:AC=AD+CE.
如图,在Rt△ABC中,∠A=90°,点D为斜边BC上一点,且BD=BA,过点D作BC的垂线交AC于点E.求证:点E在∠ABC的角平分线上.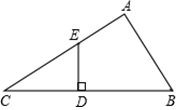
如图,AB=AC,MB=MC.求证:直线AM垂直平分线段BC.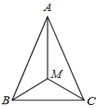
如图:点B、E、C、F在同一直线上,AB=DE,∠A=∠D,AB∥DE.
求证:△ABC≌△DEF.