如图甲,在水平桌面上固定着两根相距0.2m,相互平行的无电阻轨道P和轨道一端固定一根电阻为0.0l Ω的导体棒a,轨道上横置一根质量为40g、电阻为0.0lΩ的金属棒b,两棒相距0.2m.该轨道平面处在磁感应强度大小可以调节的竖直向上的匀强磁场中.开始时,磁感应强度B0="0.10" T(设棒与轨道间的最大静摩擦力和滑动摩擦力相等,g取10 m/s2)

(1)若从t=0开始,磁感应强度B随时间t按图乙中图象所示的规律变化,求在金属棒b开始运动前,这个装置释放的热量是多少?
(2)若保持磁感应强度B0的大小不变,从t=0时刻开始,给b棒施加一个水平向右的拉力,使它做匀加速直线运动.此拉力F的大小随时间t变化关系如图丙所示.求匀加速运动的加速度及b棒与导轨间的滑动摩擦力.
如图所示,一个半径为R的光滑圆弧轨道APB竖直固定放置,PQ为其竖直对称轴,∠AOQ与∠BOQ都等于θ。现让一可看做质点的小球在轨道内侧运动,当其冲出A点后恰好可以从B点再进入轨道,所以此运动可以周而复始进行。已知小球质量为m,重力加速度为g,试求: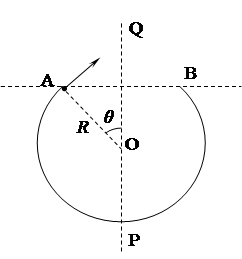
(1)小球离开轨道后的最高点距直线AB的距离;
(2)若要小球在最低点时对轨道的压力最小,θ应为多少?对应的最小压力为多少?
如图所示,在一个倾角为θ=37°(cos37°=0.8)的斜面上, O点固定一根细绳,细绳另一端连接一个质点。现将质点放到斜面上P点,由静止释放,已知OP连线水平且间距为绳长,质点滑动到细绳转过角度α=90°的位置时刚好停止。问:
(1)质点与斜面间动摩擦因数μ为多少?
(2)试描述质点放到斜面上哪些位置时可以平衡?已知最大静摩擦力与滑动摩擦力相等。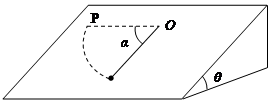
如图,在一个平面直角坐标系内,原点O处有一质点,质量为m。为使质点到达坐标为(d,d)的点P,现给质点施以大小为F的恒力,在起初的时间t1内该力方向为x轴正方向,之后的时间t2内该力变为y轴正方向,经过这两段运动质点刚好到达P点。试求:
(1)比值t1:t2;
(2)质点到达P点时的速度。
甲车停在平直公路上,乙车以速度v0=20m/s从甲车旁驶过,同时甲车启动开始追赶乙车。已知甲车的启动加速度为a=5m/s2,达到其最大速度v=30m/s后做匀速运动。试问:
(1)甲车追上乙车时是在加速阶段还是匀速阶段?
(2)甲车追上乙车一共所花的时间是多少?
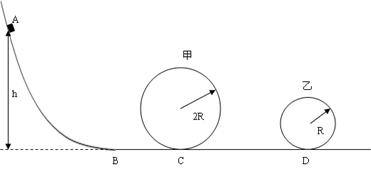
如图半径分别为2R和R的甲、乙两光滑圆形轨道固定放置在同一竖直平面内,两轨道之间由一条水平轨道CD相连,曲面轨道与水平面轨道在B处光滑连接(物块经过B点时没有机械能损失),现有一小物块从斜面上高h处的A点由静止释放,曲面轨道以及水平轨道BC段是光滑的,小物块与CD段以及D右侧的水平轨道间的动摩擦因数均为μ。已知小物块通过甲轨道最高点时与轨道间压力为物块重力的3倍,而后经过有摩擦的CD段后又进入乙轨道运动。
(1)求初始释放物块的高度h
(2)为避免出现小物块脱离圆形轨道乙而发生撞轨现象,则CD段的长度应满足什么条件?