某校设计了一个实验考查方案:考生从 道备选题中一次性随机抽取
道备选题中一次性随机抽取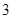 道题,按照题目要求独立完成全部实验操作.规定:至少正确完成其中
道题,按照题目要求独立完成全部实验操作.规定:至少正确完成其中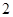 道题的便可通过.已知
道题的便可通过.已知 道备选题中考生甲有
道备选题中考生甲有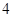 道题能正确完成,
道题能正确完成,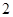 道题不能完成;考生乙每题正确完成的概率都是
道题不能完成;考生乙每题正确完成的概率都是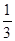 ,且每题正确完成与否互不影响.
,且每题正确完成与否互不影响.
(1)求甲、乙两考生正确完成题数的概率分布列,并计算其数学期望;
(2)请分析比较甲、乙两考生的实验操作能力.
如图,四棱锥P﹣ABCD的底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=CD,E是PC的中点.
(1)证明PA∥平面BDE;
(2)求二面角B﹣DE﹣C的平面角的余弦值;
(3)在棱PB上是否存在点F,使PB⊥平面DEF?证明你的结论.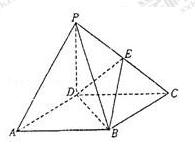
已知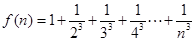 ,
,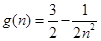 ,
,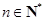 .
.
(1)当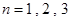 时,试比较
时,试比较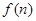 与
与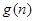 的大小关系;
的大小关系;
(2)猜想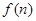 与
与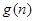 的大小关系,并给出证明.
的大小关系,并给出证明.
设函数f(x)=x3-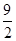 x2+6x-a.
x2+6x-a.
(1)对于任意实数x,f′(x)≥m恒成立,求m的最大值;
(2)若方程f(x)=0有且仅有一个实根,求a的取值范围.
2位男生和3位女生共5位同学站成一排,若男生甲不站两端,3位女生中有且只有两位女生相邻,则不同排法的种数是多少?
已知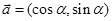 ,
, (
(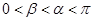 ).
).
(1)若 ,求证:
,求证: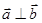 ;
;
(2)设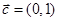 ,若
,若 ,求
,求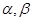 的值.
的值.