已知椭圆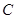 :
:
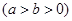 的离心率为
的离心率为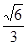 ,过右焦点
,过右焦点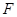 且斜率为
且斜率为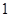 的直线交椭圆
的直线交椭圆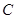 于
于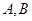 两点,
两点,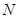 为弦
为弦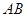 的中点,
的中点,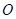 为坐标原点.
为坐标原点.
(1)求直线 的斜率
的斜率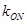 ;
;
(2)求证:对于椭圆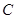 上的任意一点
上的任意一点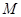 ,都存在
,都存在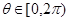 ,使得
,使得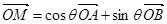 成立.
成立.
(本小题满分14分)
已知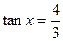 ,
,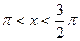 .
.
(1)若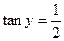 ,求证:
,求证: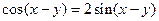 ;
;
(2)求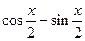 的值.
的值.
(本小题满分14分)
已知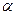 的终边经过点
的终边经过点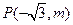 ,且
,且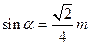 ,求
,求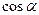 ,
,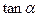 的值.
的值.
已知向量
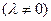 ,
,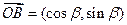 ,且
,且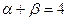 .
.
(1)求 ,
, 的夹角
的夹角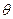 的大小;
的大小;
(2)求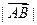 的最小值.
的最小值.

给出50个数,1,2,4,7,11,…,其规律是:第1个数是1,第2个数比第1个数大1,第3个数比第2个数大2,第4个数比第3个数大3,…,以此类推. 要求计算这50个数的和. 先将下面给出的程序框图补充完整,再根据程序框图写出伪代码.
1. 把程序框图补充完整:
(1)________________________ (4分)
(2)________________________ (4分)
2. 写出伪代码:
某次运动会甲、乙两名射击运动员成绩如下:
甲:9.4,8.7,7.5,8.4,10.1,10.5,10.7,7.2,7.8,10.8;
乙:9.1,8.7,7.1,9.8,9.7,8.5,10.1,9.2,10.1,9.1;
(1)用茎叶图表示甲,乙两个成绩;
(2)根据茎叶图分析甲、乙两人成绩;
(3)分别计算两个样本的平均数 和标准差s,并根据计算结果估计哪位运动员的成绩比较稳定.
和标准差s,并根据计算结果估计哪位运动员的成绩比较稳定.