（1）用小立方块搭成的几何体，主视图和俯视图如下图，问搭成这样的几何体最多要 小立方块，最少要 小立方块.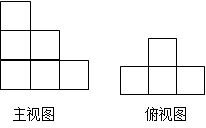
（2）世园会期间，西安某学校组织教师和学生参观世园会，每位教师的车费为m元，每位学生的车费为n元，学生每满100人可优惠2人的车费，如果该校七年级有教师20人，学生612人，则需要付给汽车公司的总费用为_______ 元.
计算或化简求值：（本题共12分，每题4分）．
（1）
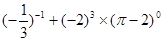
（2）
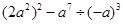
（3）
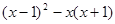
如图．等腰直角三角形ABC中，∠A=90°,P为BC的中点，小明拿着含45°角的透明三角形，使45°角的顶点落在点P，且绕P旋转．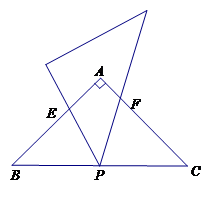
（1）如图①：当三角板的两边分别AB、AC交于E、F点时，试说明△BPE∽△CFP．
（2）将三角板绕点P旋转到图②，三角板两边分别交BA延长线和边AC于点EF．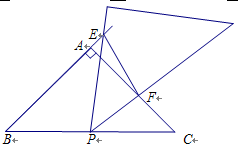
探究1：△BPE与△CFP．还相似吗？（只需写结论）
探究2：连接EF，△BPE与△EFP是否相似？请说明理由．
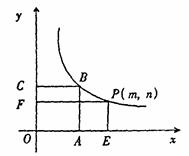
如图所示，已知正方形
的面积为9 ，点
在函数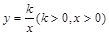
的图象上,点
（
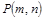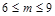）是函数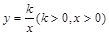的图象上动点，过点
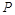分别作
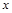轴、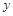
轴的垂线，垂足分别为
、
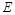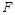，若设矩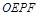形
和正方形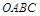不重合的两部分的面积和为
。
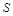(1)求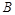点坐标和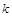
的值；(2)写出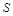关于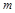
的函数关系和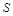的最大值。
跃壮五金商店准备从宁云机械厂购进甲、乙两种零件进行销售．若每个甲种零件的进价比每个乙种零件的进价少2元，且用80元购进甲种零件的数量与用100元购进乙种零件的数量相同．
(1)求每个甲种零件、每个乙种零件的进价分别为多少元?
(2)若该五金商店本次购进甲种零件的数量比购进乙种零件的数量的3倍还少5个，购进两种零件的总数量不超过95个，该五金商店每个甲种零件的销售价格为12元，每个乙种零件的销售价格为15元，则将本次购进的甲、乙两种零件全部售出后，可使销售两种零件的总利润(利润=售价－进价)超过371元，通过计算求出跃壮五金商店本次从宁云机械厂购进甲、乙两种零件有几种方案?请你设计出来．
如图①，
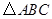为等边三角形，周长为p．
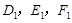分别是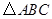三边的中点，连结
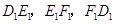，可得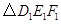
．
（1）用p表示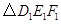的周长是；
（2）当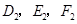
分别是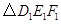三边的中点，如图②，则
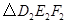的周长是_______；（用含p的式子表示）
（3）按照上述思路探索下去，当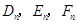
分别是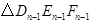
三边的中点时（
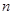为正整数），
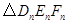的周长是．（用含n、p的式子表示）