如图,直线AC∥BD,连结AB,直线AC、BD及线段AB把平面分成①、②、③、④四个部分,规定:线上各点不属于任何部分.当动点P落在某个部分时,连结PA、PB,构成∠PAC、∠APB、∠PBD三个角. (提示: 有公共端点的两条重合的射线所组成的角是0°)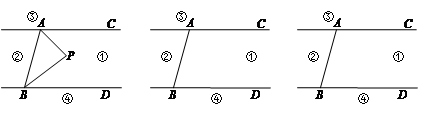
(1)当动点P落在第①部分时,有∠APB=∠PAC+∠PBD,请说明理由;
(2)当动点P落在第②部分时,∠APB=∠PAC+∠PBD是否成立?若不成立,试写出∠PAC、∠APB、∠PBD三个角的关系(无需说明理由);
(3)当动点P在第③部分时,探究∠PAC、∠APB、∠PBD之间的关系,写出你发现的一个结论并加以说明.
解方程:
(1)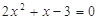
(2)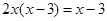
如图,直线y=x+3的图象与x轴、y轴交于A、B两点.直线l经过原点,与线段AB交于点C,把△AOB的面积分为2:1两部分.求直线l的解析式.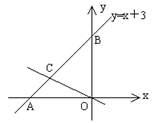
如图四边形ABCD是实验中学的一块空地的平面图,其中∠B=90°,AB=3m,BC=4m,CD=12m,AD=13m现计划在空地上植上草地绿化环境,若每平方米的草皮需150元;问需投入资金多少元?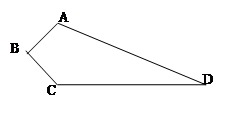
已知,边长为6的等边三角形ABC,建立适当的直角坐标系,
(1)写出各个顶点的坐标.
(2)求出这个等边三角形的面积.
已知一次函数图象经过A(-2,-3),B(1,3)两点.
(1)求这个一次函数解析式.
(2)试判断点P(-1,1)是否在这个一次函数的图象上?