提高大桥的车辆通行能力可改善整个城市的交通状况．一般情况下，大桥上的车流
速度v(单位：千米/小时)是车流密度x(单位：辆/千米)的函数．当车流密度不超过50辆/千米时，车流速度为30千米/小时．研究表明：当50＜x≤200时，车流速度v与车流密度x满足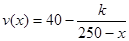
．当桥上的车流密度达到200辆/千米时，造成堵塞，此时车流速度为0千米/小时．
（Ⅰ）当0<x≤200时，求函数v(x)的表达式；
（Ⅱ）当车流密度x为多大时，车流量(单位时间内通过桥上观测点的车辆数，单位：
辆/小时)f(x)＝x·v(x)可以达到最大，并求出最大值．(精确到个位，参考数据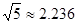
）
已知函数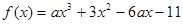
，
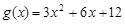，和直线m:y=kx+9，又
．
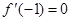（1）求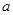
的值；
（2）是否存在k的值，使直线m既是曲线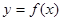
的切线，又是
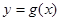的切线；如果存在，求出k的值；如果不存在,说明理由．
（3）如果对于所有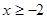
的
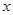,都有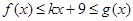
成立，求k的取值范围．
数列{ a n}满足a 1＋2 a 2＋22 a 3＋…＋2n－1 a n＝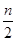
，（n∈N*）前n项和为Sn；数列{bn}是等差数列，且b1=2，其前n项和Tn满足
（
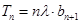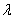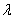为常数，且<1）．
（1）求数列{ a n}的通项公式及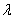的值；
（2）设
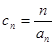，求数列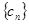
的前n项的和
；
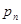（3）证明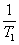
+
+
+ +
>
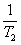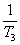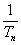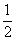Sn．
已知函数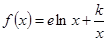
（其中e是自然对数的底数，k为正数）
（1）若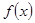
在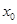
处取得极值，且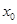是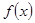的一个零点，求k的值；
（2）若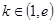
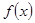，求在区间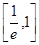
上的最大值；
（3）设函数g（x）=f（x）-kx在区间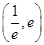
上是减函数，求k的取值范围.
已知
设函数f（x）=
的图像关于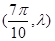
对称,其中
，
为常数,且∈
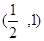
（1）求函数f（x）的最小正周期T；
（2）函数过
求函数在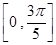
上取值范围。
在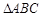
中，已知
．
（1）求证：tanB=3tanA
（2）若
求A的值．