已知函数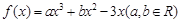 ,且
,且 在
在 和
和 处取得极值.
处取得极值.
(1)求函数 的解析式.
的解析式.
(2)设函数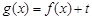 ,是否存在实数
,是否存在实数 ,使得曲线
,使得曲线 与
与 轴有两个交点,若存在,求出
轴有两个交点,若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
已知曲线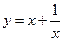 上一点
上一点 ,用斜率定义求:
,用斜率定义求:
(1)点A的切线的斜率
(2)点A处的切线方程
求曲线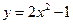 的斜率等于4的切线方程.
的斜率等于4的切线方程.
(本小题共12分)已知函数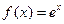 (
( 为自然对数的底数),
为自然对数的底数),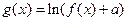 (
( 为常数),
为常数), 是实数集
是实数集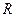 上的奇函数.(Ⅰ)求证:
上的奇函数.(Ⅰ)求证: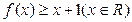 ;
;
(Ⅱ)讨论关于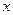 的方程:
的方程: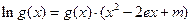
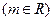 的根的个数;
的根的个数;
(Ⅲ)设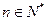 ,证明:
,证明: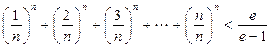 (
( 为自然对数的底数).
为自然对数的底数).
(本小题共12分)已知数列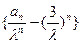 是等差数列,公差为2,
是等差数列,公差为2,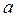 1,=11,
1,=11,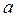 n+1=λ
n+1=λ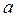 n+bn.
n+bn.
(Ⅰ)若 的值;(Ⅱ)在(Ⅰ)条件下,求数列{
的值;(Ⅱ)在(Ⅰ)条件下,求数列{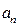 }的前n项和.
}的前n项和.
(本小题满分12分)已知椭圆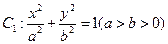 的左、右焦点分别为
的左、右焦点分别为 、
、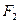 ,其中
,其中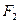 也是抛物线
也是抛物线 的焦点,
的焦点, 是
是 与
与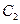 在第一象限的交点,且
在第一象限的交点,且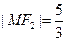 .(Ⅰ)求椭圆
.(Ⅰ)求椭圆 的方程;(Ⅱ)已知菱形
的方程;(Ⅱ)已知菱形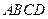 的顶点A﹑C在椭圆
的顶点A﹑C在椭圆 上,顶点B﹑C在直线
上,顶点B﹑C在直线 上,求直线
上,求直线 的方程.
的方程.