如图,在平面直角坐标系xOy中,二次函数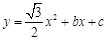 的图象与
的图象与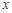 轴交于
轴交于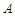 (-1,0)、
(-1,0)、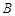 (3,0)两点, 顶点为
(3,0)两点, 顶点为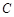 .
.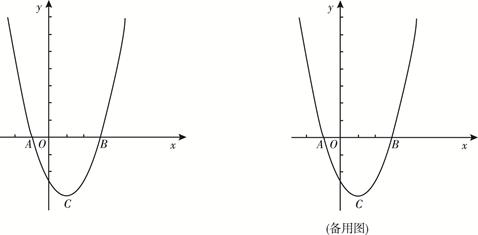
(1) 求此二次函数解析式;
(2) 点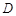 为点
为点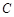 关于x轴的对称点,过点
关于x轴的对称点,过点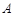 作直线
作直线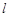 :
: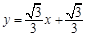 交BD于点E,过点
交BD于点E,过点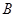 作直线
作直线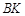 ∥
∥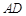 交直线
交直线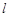 于
于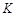 点.问:在四边形ABKD的内部是否存在点P,使得它到四边形ABKD四边的距离都相等,若存在,请求出点P的坐标;若不存在,请说明理由;
点.问:在四边形ABKD的内部是否存在点P,使得它到四边形ABKD四边的距离都相等,若存在,请求出点P的坐标;若不存在,请说明理由;
(3) 在(2)的条件下,若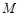 、
、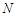 分别为直线
分别为直线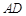 和直线
和直线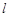 上的两个动点,连结
上的两个动点,连结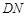 、
、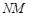 、
、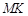 ,求
,求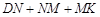 和的最小值.
和的最小值.
商场某种商品平均每天可销售30件,每件盈利50元,为了尽快减少库存,商场决定采取适当的降价措施,经调查发现,每件商品每降价1元,商场每天可多售出2件,设每件商品降低x元据此规律,请回答:
(1)商场日销售量增加 件,每件商品盈利 元(用含x的代数式表示)
(2)在上述条件不变,销售正常的情况下,每件商品降价多少元时,商场日盈利可达到2100元?
如图,在⊙O中,∠ACB=∠BDC=60°,AC=2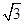 cm.
cm.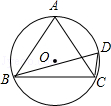
(1)求∠BAC的度数;
(2)求⊙O的周长.
已知关于x的一元二次方程x2+(2k+1)x+k2-2=0有实根
(1)求k的取值范围
(2)若方程的两实根的平方和等于11,求k的值.
小明家的房前有一块矩形的空地,空地上有三棵树A、B、C,小明想建一个圆形花坛,使三棵树都在花坛的边上.
(1)请你帮小明把花坛的位置画出来(尺规作图,不写作法,保留作图痕迹);
(2)若△ABC中AB=8米,AC=6米,∠BAC=90°,试求小明家圆形花坛的面积.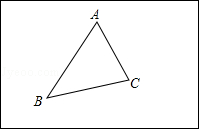
用适当的方法解下列方程
(1)(x-2)2-4=0
(2)x2-4x-3=0
(3)3(x-2)2=x(x-2)
(4)x2+4x-5=0(配方法)
(5)x2+2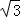 x+3=0.
x+3=0.