如图1，在平面直角坐标系中，点A、C分别在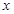
轴、
轴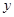上，四边形OABC是面积为4的正方形，函数
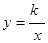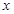(＞0)的图象经过点B．
（1）
= ；
（2）如图2，将正方形OABC分别沿直线AB、BC翻折，得到正方形MABC′和正方形MA′BC．设线段MC′、NA′分别与函数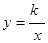 (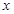＞0)的图象交于点E、F，则点E、F的坐标分别为：E （ ， ） ，F （ ， ）；
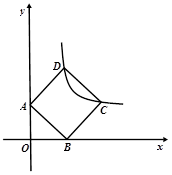
（3）如图3，面积为4的正方形ABCD的顶点A、B分别在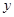轴、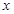轴上，顶点C、D在反比例函数
（＞０）的图像上，试求ＯＡ、ＯＢ的长。（请写出必要的解题过程）
如图，平行四边形ABCD的对角线AC的延长线上取两点E、F，使EA＝CF．求证：四边形EBFD是平行四边形． 
请用适当的方法解下列方程：
（1）2(x－4)2＝18
（2）4x2－4x－3=0
（1）
－
＋
（2）
如图，凸四边形ABCD中，点E在边CD上，连接AE、BE．给出下列五个关系式:①AD∥BC；②DE=EC； ③∠1=∠2；④∠3＝∠4；⑤AD+BC="AB" .将其中的三个关系式作为已知条件、另外两个关系式作为结论，可以构成一些命题（下面各小题的命题须符合此要求）．
(1)共计能够成个命题；
(2)写出三个真命题：
①如果、、，那么、；
②如果、、，那么、；
③如果、、，那么、.
请选择上述三个命题中的一个写出它是真命题的理由：
证明：我选择证明命题（填序号），理由如下：
（第28题图）
(3)请写出一个假命题（不必说明理由）：
如果、、，那么、.
（1）探究新知：如图1，已知△ABC与△ABD的面积相等， 试判断AB与CD的位置关系，并说明理由．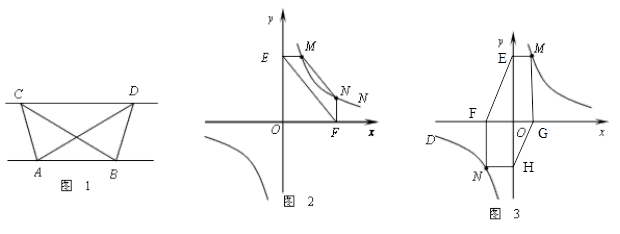 
（2）结论应用：如图2，点M，N在反比例函数
（k＞0）的图象上，过点M作ME⊥y轴，过点N作NF⊥x轴，垂足分别为E，F． 试证明：MN∥EF．
（3）变式探究：如图3，点M，N在反比例函数（k＞0）的图象上，过点M作ME⊥y轴，过点N作NF⊥x轴，过点M作MG⊥x轴，过点N作NH⊥y轴，垂足分别为E、F、G、H． 试证明：EF ∥GH．