如图所示,一位质量m=60kg的队员,在参加一次消防逃生演练中,队员从倾斜直滑道AB的顶端A由静止滑下,经B点后水平滑出,最后落在水平地面的护垫上(不计护垫厚度的影响)。已知A、B离水平地面的高度分别为H=6.2m、h=3.2m,A、B两点间的水平距离为L=4.0m,队员落地点到B点的水平距离为s=4.8m,g取10m/s2。求: 
(1)队员到达B点的速度大小;
(2)队员与滑道间的动摩擦因数μ;
如图所示,斜面轨道AB与水平面之间的夹角θ=53O,BD为半径R =" 4" m的圆弧形轨道,且B点与D点在同一水平面上,在B点,轨道AB与圆弧形轨道BD相切,整个轨道处于竖直平面内且处处光滑,在A点处的一质量m=1kg的小球由静止滑下,经过B、C点后从D点斜抛出去,最后落在地面上的S点处时的速度大小vS= 8m/s,已知A点距地面的高度H = 10m,B点距地面的高度h ="5" m,设以MDN为分界线,其左边为一阻力场区域,右边为真空区域,g取10m/s2, ,
,
(1)小球经过C点的速度为多大?
(2)小球从D点抛出后,受到的阻力f与其瞬时速度方向始终相反,求小球从D点至S点的过程中,阻力f所做的功.
如图所示电路,U恒为10V、R1=4Ω、R2=6Ω、C1=C2=30μF,先闭合开关S,待电路稳定后再断开S,求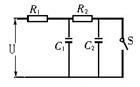
(1)闭合开关S稳定后,C1上的电量;
(2)断开开关S稳定后,C2上的电量
(3)从闭合S稳定到断开S稳定过程中,通过电阻R2、R1的电荷量.
如图所示,固定在竖直面内的光滑半圆形轨道与粗糙水平轨道在B点平滑连接,轨道半径R=0.5m,一质量m=0.2kg的小物块(可视为质点)放在水平轨道上的A点,A与B相距L=10m,物块与水平轨道间的动摩擦因数μ=0.1。现用一水平恒力F向右推物块,已知F=3N,当物块运动到C点时撤去该力,设C点到A点的距离为x。在圆轨道的最高点D处安装一压力传感器,当物块运动到D点时传感器就会显示相应的读数FN,压力传感器所能承受的最大压力为90N,g取10m/s2。
(1)要使物块能够安全通过圆轨道的最高点D,求x的范围;
(2)在满足(1)问的情况下,在坐标系中作出压力传感器的读数FN与x的关系图象。
如图所示,两带有等量异电荷的平行金属板M、N竖直放置,M、N两板间的距离d=0.5m.现将一质量为m=1×10-2kg、电荷量q=4×10-5C的带电小球从两极板上方A点以v0=4m/s的初速度水平抛出,A点距离两板上端的高度h=0.2m,之后小球恰好从靠近M板上端处进入两板间,沿直线运动碰到N板上的B点,不计空气阻力,取g=10m/s2.设匀强电场只存在于M、N之间。求:
(1)两极板间的电势差;
(2)小球由A到B所用总时间;
(3)小球到达B点时的动能.
如图所示,abcd是一个正方形盒子.cd边的中点有一个小孔e.盒子中有沿ad方向的匀强电场.一个质量为m带电粒子从a处的小孔沿ab方向以初速度v0射入盒内,并恰好从e处的小孔射出.求:(1)该带电粒子从e孔射出时的速度大小.(2)该过程中电场力对该带电粒子做的功.