走廊里的一盏电灯由走廊两端的两开关控制,不管哪个开关接通都能使电灯点亮,则设计的电路为( )
| A.“与”门电路 | B.“非”门电路 | C.“或”门电路 | D.“与非”门电路 |
如图,质量为m的物块始终静止在倾角为θ的斜面上,则()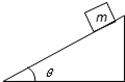
| A.若斜面向左匀速移动距离s,则斜面对物块做功为mgsinθcosθs |
| B.若斜面向上匀速移动距离s,则斜面对物块做功为mgs |
| C.若斜面向左以加速度a匀加速移动距离s,则斜面对物块不做功 |
| D.若斜面向上以加速度a匀加速移动距离s,则斜面对物块做功为mas |
宇宙飞船绕地球做匀速圆周运动,先在半径为R1的轨道上运行,变轨后在半径为R2的轨道上运行,R1>R2,则变轨后宇宙飞船的()
| A.线速度变大 | B.角速度变小 |
| C.向心加速度变小 | D.周期变大 |
如图所示,两平行金属板竖直放置,板上A、B两孔正好水平相对,板间电压为500V.一个动能为400 eV的电子从A孔沿垂直板方向射入电场中.经过一段时间电子离开电场,则电子离开电场时的动能大小为 ()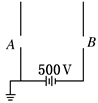
A.400 eV B.500 eV C.900 eV D.100 eV
两个完全相同的小金属球(皆可视为点电荷),所带电荷量之比为5∶1,它们在相距一定距离时相互作用的吸引力为F1,如果让它们充分接触后再放回各自原来的位置上,此时相互作用力变为F2,则F1∶F2为()
| A.5∶2 | B.5∶4 | C.5∶6 | D.5∶9 |
质量为2 kg的质点在x-y平面上做曲线运动,在x方向的速度图象和y方向的位移图象如图所示,下列说法正确的是()
| A.质点的初速度为3 m/s |
| B.2 s末质点速度大小为6 m/s |
| C.质点做曲线运动的加速度为3m/s2 |
| D.质点所受的合外力为3 N |