如图,某城市设立以城中心 为圆心、
为圆心、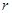 公里为半径的圆形保护区,从保护区边缘起,在城中心
公里为半径的圆形保护区,从保护区边缘起,在城中心 正东方向上有一条高速公路
正东方向上有一条高速公路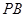 、西南方向上有一条一级公路
、西南方向上有一条一级公路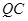 ,现要在保护区边缘PQ弧上选择一点A作为出口,建一条连接两条公路且与圆
,现要在保护区边缘PQ弧上选择一点A作为出口,建一条连接两条公路且与圆 相切的直道
相切的直道 .已知通往一级公路的道路
.已知通往一级公路的道路 每公里造价为
每公里造价为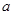 万元,通往高速公路的道路
万元,通往高速公路的道路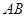 每公里造价是
每公里造价是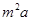 万元,其中
万元,其中 为常数,设
为常数,设 ,总造价为
,总造价为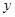 万元.
万元.
(1)把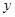 表示成
表示成 的函数
的函数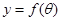 ,并求出定义域;
,并求出定义域;
(2)当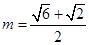 时,如何确定A点的位置才能使得总造价最低?
时,如何确定A点的位置才能使得总造价最低?
汶川震后在社会各界的支持和帮助下,汶川一中临时搭建了学校,学校餐厅也做到了保证每天供应1000名学生用餐,每星期一有A、B两样菜可供选择(每个学生都将从二者中选一),为了让学生们能够安心上课对学生的用餐情况进行了调查。调查资料表明,凡是在本周星期一选A菜的,下周星期一会有20%改选B,而选B菜的,下周星期一则有30%改选A,若用A 、B
、B 分别表示在第n个星期一选A、B菜的人数。
分别表示在第n个星期一选A、B菜的人数。
(1)试以A 表示A
表示A ;
;
(2)若A =200,求{A
=200,求{A }的通项公式;
}的通项公式;
(3)问第n个星期一时,选A与选B的人数相等?
已知向量 ,
,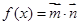 .
.
(I)若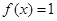 ,求
,求 值;
值;
(II)在 中,角
中,角 的对边分别是
的对边分别是 ,且满足
,且满足 ,求函数
,求函数 的取值范围.
的取值范围.
已知奇函数
(1)试确定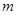 的值;
的值;
(2)若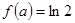 ,求
,求 的值;
的值;
(3)求函数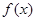 在
在 上的最小值.
上的最小值.
经过调查发现,某一时尚产品在投放市场的30天中,前20天其价格呈直线上升,后10天价格呈直线下降趋势。现抽取其中4天的价格如下表所示:
| 时间 |
第4天 |
第12天 |
第21天 |
第28天 |
| 价格(百元) |
34 |
42 |
48 |
34 |
(1)写出价格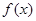 关于时间
关于时间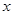 的函数表达式(
的函数表达式(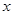 表示投放市场的第
表示投放市场的第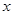 天);
天);
(2)若销售量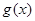 与时间
与时间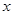 的函数关系式为:
的函数关系式为: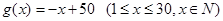 ,问该产品投放市场第几天,日销售额最高?
,问该产品投放市场第几天,日销售额最高?
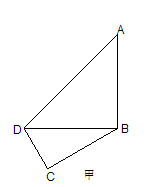
如图甲,在平面四边形ABCD中,已知
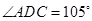 ,
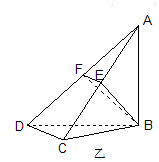
,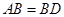 ,现将四边形ABCD沿BD折起,使平面ABD
,现将四边形ABCD沿BD折起,使平面ABD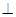 平面BDC(如图乙),设点E、F分别为棱AC、AD的中点.
平面BDC(如图乙),设点E、F分别为棱AC、AD的中点.
(Ⅰ)求证:DC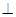 平面ABC;
平面ABC;
(Ⅱ)设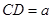 ,求三棱锥F-ABE的体积.
,求三棱锥F-ABE的体积.