如图，在平面直角坐标系中，二次函数y=ax2+6x+c的图象经过点A（4，0）、B（﹣1，0），与y轴交于点C，点D在线段OC上，OD=t，点E在第二象限，∠ADE=90°，tan∠DAE=，EF⊥OD，垂足为F．
（1）求这个二次函数的解析式；
（2）求线段EF、OF的长（用含t的代数式表示）；
（3）当△ECA为直角三角形时，求t的值．
九年级（1）班的学生周末乘汽车到游览区游览，游览区到学校120千米，一部分学生乘慢车先行，出发1小时后，另一部分学生乘快车前往，结果他们同时到达，已知快车速度是慢车速度的1.5倍，求慢车的速度．
已知：如图，在△ABC中，∠ACB=90°点D是AB的中点，延长BC到点F，延长CB到点E，使CF=BE，联结DE、DC、DF求证：DE=DF．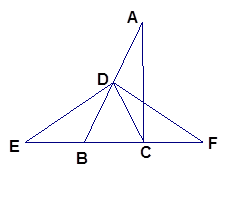
解不等式
，并把它的解集在数轴上表示出来．
计算：
．
如图，在平面直角坐标系中，直线
分别交
轴，
轴于
两点，以
为边作矩形
，
为
的中点．以
，
为斜边端点作等腰直角三角形
，点
在第一象限，设矩形
与
重叠部分的面积为
．
求点
的坐标；当
值由小到大变化时，求与的函数关系式；若在直线
上存在点
，使
等于
，请直接写出的取值范围在
值的变化过程中，若
为等腰三角形，且PC=PD，请直接写出的值．