已知向量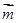 =(sinB,1-cosB),且与向量
=(sinB,1-cosB),且与向量 =(2,0)所成角为
=(2,0)所成角为 ,其中A、B、C是△ABC的内角。
,其中A、B、C是△ABC的内角。
(1)求角B的大小;
(2)求sinA+sinC的取值范围。
已知函数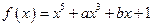 在
在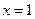 和
和 处取得极值.
处取得极值.
(1)求 和
和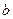 的值;
的值;
(2)求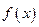 的单调区间
的单调区间
已知三点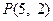 ,
,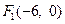 ,
,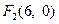 .
.
(1)求以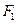 ,
,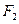 为焦点,且过点
为焦点,且过点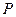 的椭圆方程;
的椭圆方程;
(2)设点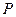 ,
,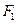 ,
,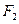 关于直线
关于直线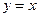 的对称点分别为
的对称点分别为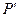 ,
, ,
,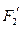 ,求以
,求以 ,
,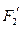 为焦点,且过点
为焦点,且过点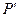 的双曲线方程.
的双曲线方程.
用边长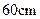 的正方形的铁皮做一个无盖水箱,先在四角分别截去相同的小正方形,然后把四边翻转
的正方形的铁皮做一个无盖水箱,先在四角分别截去相同的小正方形,然后把四边翻转 再焊接而成.问水箱底边应取多少,才能使水箱的容积最大?
再焊接而成.问水箱底边应取多少,才能使水箱的容积最大?
数列{an}中, .(Ⅰ)求
.(Ⅰ)求 ;
;
(Ⅱ)猜想 的表达式,并用数学归纳法加以证明.
的表达式,并用数学归纳法加以证明.
已知某射手射击一次,击中目标的概率是 .(1)求连续射击5次,恰有3次击中目标的概率;
.(1)求连续射击5次,恰有3次击中目标的概率;
(2)求连续射击5次,击中目标的次数X的数学期望和方差.
(3)假设连续2次未击中目标,则中止其射击,求恰好射击5次后,被中止射击的概率.(本题结果用分数表示即可).