如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,-2)。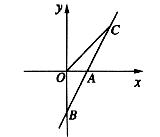
(1)求直线AB的函数表达式;
(2)若直线AB上的点C在第一象限,且S△BOC=2,求点C的坐标。
如图,大海中有A和B两个岛屿,为测量它们之间的距离,在海岸线PQ上点E处测得∠AEP=74°,∠BEQ=30°;在点F处测得∠AFP=60°,∠BFQ=60°,EF=1km.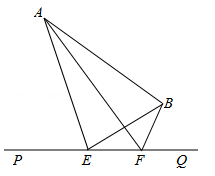
(1)判断线段AB与AE的数量关系,并说明理由;
(2)求两个岛屿A和B之间的距离(结果精确到0.1km).
甲、乙两商场同时开业,为了吸引顾客,都举办有奖酬宾活动,凡购物满100元,均可得到一次摸奖的机会.在一个纸盒里装有2个红球和2个白球,除颜色外,其他全部相同,摸奖者一次从中摸出两个球,根据球的颜色决定送礼金券的多少(如下表).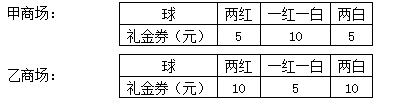
(1)请你用列表法(或画树状图)求出摸到一红一白的概率;
(2)如果只考虑中奖因素,你将会选择去哪个商场购物?请说明理由.
(本题8分)某校八年级所有学生参加2013年初中生物竞赛,我们从中随机抽取了部分学生的考试成绩,将他们的成绩进行统计后分为A、B、C、D四等,并将统计结果绘制成如下的统计图,请你结合图中所给信息解答下列问题: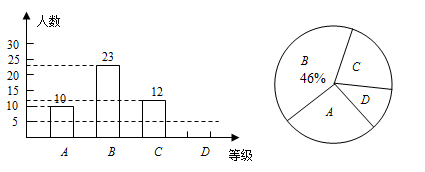
(说明:A级:25分~30分;B级:20分~24分;C级:15分~19分;D级:15分以下)
(1)请把条形统计图补充完整;
(2)扇形统计图中D级所占的百分比是_______ ;
(3)扇形统计图中A级所在的扇形的圆心角度数是_______ ;
(4)若该校九年级有850名学生,请你估计全年级A级和B级的学生人数共约为______ 人.
如图,在□ABCD中,E、F为BC上的两点,且 BE=CF,AF=DE.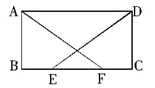
求证:(1)△ABF≌△DCE;
(2)四边形ABCD是矩形.
(1)解方程: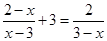 ;
;
(2) 解不等式组: .
.