如图，已知椭圆C：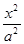
+
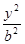=1（a>b>0）的左、右焦点分别为F
、F
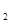，A是椭圆C上的一点，A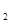F⊥FF，O是坐标原点，OB垂直AF于B，且OF=3OB.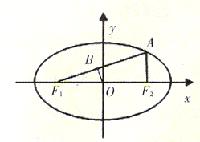
（Ⅰ）求椭圆C的离心率；
（Ⅱ）求t∈（0，b），使得命题“设圆x
+y=t上任意点M（x
，y）处的切线交椭圆C于Q、Q两点，那么OQ⊥OQ”成立.
把4个球随机地投入4个盒子中去，设ξ表示空盒子的个数，求Eξ、Dξ.
人寿保险中（某一年龄段），在一年的保险期内，每个被保险人需交纳保费a元，被保险人意外死亡则保险公司赔付3万元，出现非意外死亡则赔付1万元.经统计此年龄段一年内意外死亡的概率是p1，非意外死亡的概率为p2，则a需满足什么条件，保险公司才可能盈利?
设ξ是一个离散型随机变量，其分布列如下表，试求Eξ、Dξ.
| ξ |
－1 |
0 |
1 |
| P |
 |
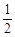1－2q |
q2 |
有甲乙两个箱子，甲箱中有6个小球，其中1个标记0号，2个小球标记1号，3个小球标记2号；乙箱装有7个小球，其中4个小球标记0号，一个标记1号，2个标记2号。从甲箱中取一个小球，从乙箱中取2个小球，一共取出3个小球。求：
（1）取出的3个小球都是0号的概率；
（2）取出的3个小球号码之积是4的概率；
某厂生产电子元件，其产品的次品率为5%，现从一批产品中的任意连续取出2件，求次品数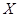
的概率分布