如图,在直角梯形ABCD中,AB∥DC,∠D=90o,AC⊥BC,AB=10cm,BC=6cm,F点以2cm/秒的速度在线段AB上由A向B匀速运动,E点同时以1cm/秒的速度在线段BC上由B向C匀速运动,设运动时间为t秒(0<t<5).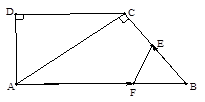
(1)求证:△ACD∽△BAC;
(2)求DC的长;
(3)设四边形AFEC的面积为y,求y 关于t的函数关系式,并求出y的最小值.
半径为5的⊙O中,直径AB的不同侧有定点C和动点P. 已知BC∶CA=4∶3,点P在弧AB上运动,过点C作CP的垂线,与PB的延长线交于点Q. 求证:△ABC∽△PQC;
当点P与点C关于AB对称时,求CQ的长;
当点P运动到什么位置时,CQ取到最大值?求此时CQ的长;
当点P运动到弧AB的中点时,求CQ的长.

直线y=-x+6与坐标轴分别交于A、B两点,动点P、Q同时从O点匀速出发,同时到达A点时运动停止.点Q沿线段OA运动,速度为每秒1个单位长度,点P沿路线O→B→A运动.
直接写出A、B两点的坐标;
设点Q的运动时间为t秒,△OPQ的面积为S,求出S与t之间的函数关系式;
当s= 时,求出点P的坐标,并直接写出以点O、P、Q为顶点的平行四边形的
第四个顶点M的坐标.
在△ABC中, AB、BC、AC三边的长分别为、、,求这个三角形的面积.小华同学在解答这道题时,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.这种方法叫做构图法.△ABC的面积为:.
若△DEF三边的长分别为、2、,请在图2的正方形网格中画出相应的△DEF,并利用构图法求出它的面积.


利用第2小题解题方法完成下题:如图3,一个六边形的花坛被分割成7个部分,其中正方形PRBA,RQDC,QPFE的面积分别为13、10、17,且△PQR、△BCR、△DEQ、△AFP的面积相等,求六边形花坛ABCDEF的面积.

无锡市南长区某桶装水经营部每天的房租、人员工资等固定成本为250元,每桶水的进价是5元,规定销售单价不得高于12元/桶,也不得低于7元/桶,调查发现日均销售量p(桶)与销售单价x(元)的函数图象如图所示.求日均销售量p(桶)与销售单价x(元)的函数关系;
若该经营部希望日均获利1350元,请你根据以上信息,就该桶装水的销售单价或销售数量,提出一个用一元二次方程解决的问题,并写出解答过程.

如图所示,AB是⊙O的一条弦,OD⊥AB,垂足为C,交⊙O于点D,点E在⊙O上.
若∠AOD =52º,求∠DEB的度数;
若OC=3,OA=5,求AB的长.