现有甲、乙两个靶。某射手向甲靶射击一次，命中的概率为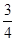
，命中得1分，没有命中得0分；向乙靶射击两次，每次命中的概率为
,每命中一次得2分，没有命中得0分。该射手每次射击的结果相互独立。假设该射手完成以上三次射击。
（Ⅰ）求该射手恰好命中一次的概率；
（Ⅱ）求该射手的总得分X的分布列及数学期望EX.
（本小题满分12分）已知函数
的最大值为
．
（1）求常数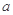
的值；
（2）求函数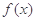
的单调递增区间；
（3）若将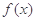的图象向左平移
个单位，得到函数
的图象，求函数在区间
上的最大值和最小值．
（本小题满分10分）设函数
.
（1）求函数
的最小值；
（2）若
,使得不等式
成立，求实数
的取值范围.
（本小题满分12分）设函数
,
,（
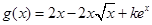是自然对数的底数）.
（1）讨论
在其定义域上的单调性；
（2）若
，且不等式
对于
恒成立，求
的取值范围.
（本小题满分12分）已知椭圆C:
短轴的两个顶点与右焦点的连线构成等边三角形，直线
与以椭圆C的上顶点为圆心，以椭圆C的长半轴长为半径的圆相切.
（1）求椭圆C的方程;
（2）椭圆C与
轴负半轴交于点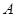
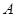，过点的直线
，
分别与椭圆C交于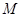
，
两点, 
分别为直线、的斜率， 
，求证：直线
过定点,并求出该定点坐标;
（3）在（2）的条件下，求
面积的最大值.
（本小题满分12分）如图，四棱锥中， ∥,，侧面为等
边三角形. 
. 
（1）证明：
；
（2）求二面角
的余弦值.