规定 ,其中
,其中 ,
, 为正整数,且
为正整数,且 ,这是排列数
,这是排列数 (
( 是正整数,且
是正整数,且 )的一种推广.
)的一种推广.
(1)求 的值;
的值;
(2)排列数的两个性质:① ,②
,② (其中
(其中 是正整数).是否都能推广到
是正整数).是否都能推广到 (
( ,m是正整数)的情形?若能推广,写出推广的形式并给予证明;若不能,则说明理由;
,m是正整数)的情形?若能推广,写出推广的形式并给予证明;若不能,则说明理由;
(3)确定函数 的单调区间.
的单调区间.
△ABC中,a,b,c分别是角A,B,C的对边, ,且
,且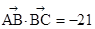 ,
,
(Ⅰ)求△ABC的面积;(Ⅱ)若a=7,求角∠C
已知函数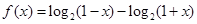 ,
,
(1)求函数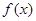 的定义域;
的定义域;
(2)判断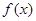 的奇偶性;
的奇偶性;
(3)方程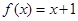 是否有根?如果有根
是否有根?如果有根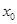 ,请求出一个长度为
,请求出一个长度为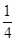 的区间
的区间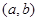 ,使
,使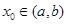 ;如果没有,请说明理由?(注:区间
;如果没有,请说明理由?(注:区间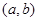 的长度
的长度 ).
).
已知两直线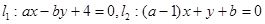 ,求分别满足下列条件的
,求分别满足下列条件的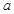 、
、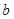 的值.
的值.
(1)直线 过点
过点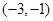 ,并且直线
,并且直线 与直线
与直线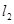 垂直;
垂直;
(2)直线 与直线
与直线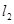 平行,并且坐标原点到
平行,并且坐标原点到 、
、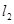 的距离相等.
的距离相等.
已知甲、乙两个工厂在今年的1月份的利润都是6万元,且甲厂在2月份的利润是14万元,乙厂在2月份的利润是8万元。若甲、乙两个工厂的利润(万元)与月份 之间的函数关系式分别符合下列函数模型:
之间的函数关系式分别符合下列函数模型: ,
, ,
,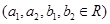 .
.
(1)求甲、乙两个工厂今年5月份的利润;
(2)在同一直角坐标系下画出函数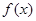 与
与 的草图,并根据草图比较今年甲、乙两个工厂的利润的大小情况.
的草图,并根据草图比较今年甲、乙两个工厂的利润的大小情况.
已知 中
中 ,
,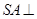 面
面 ,
,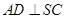 ,求证:
,求证: 面
面 .
.