已知函数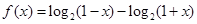 ,
,
(1)求函数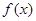 的定义域;
的定义域;
(2)判断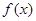 的奇偶性;
的奇偶性;
(3)方程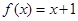 是否有根?如果有根
是否有根?如果有根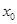 ,请求出一个长度为
,请求出一个长度为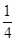 的区间
的区间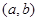 ,使
,使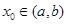 ;如果没有,请说明理由?(注:区间
;如果没有,请说明理由?(注:区间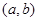 的长度
的长度 ).
).
已知函数 (
( ).
).
(1)当 时,求
时,求 的图象在
的图象在 处的切线方程;
处的切线方程;
(2)若函数 在
在 上有两个零点,求实数
上有两个零点,求实数 的取值范围;
的取值范围;
(3)若函数 的图象与
的图象与 轴有两个不同的交点
轴有两个不同的交点 ,且
,且 ,求证:
,求证: (其中
(其中 是
是 的导函数).
的导函数).
如图,矩形ABCD中,|AB|=4,|BC|=2,E,F,M,N分别是矩形四条边的中点,G,H分别是线段ON,CN的中点.
(1)证明:直线EG与FH的交点L在椭圆W: 上;
上;
(2)设直线l: 与椭圆W:
与椭圆W: 有两个不同的交点P,Q,直线l与矩形ABCD有两个不同的交点S,T,求
有两个不同的交点P,Q,直线l与矩形ABCD有两个不同的交点S,T,求 的最大值及取得最大值时m的值.
的最大值及取得最大值时m的值.
某家电专卖店在五一期间设计一项有奖促销活动,每购买一台电视,即可通过电脑产生一组3个数的随机数组,根据下表兑奖:
| 奖次 |
一等奖 |
二等奖 |
三等奖 |
| 随机数组的特征 |
3个1或3个0 |
只有2个1或2个0 |
只有1个1或1个0 |
| 资金(单位:元) |
5m |
2m |
m |
商家为了了解计划的可行性,估计奖金数,进行了随机模拟试验,并产生了20个随机数组,试验结果如下:
247,235,145,124,754,353,296,065,379,118,520,378,218,953,254,368,027,111,358,279.
(1)在以上模拟的20组数中,随机抽取3组数,至少有1组获奖的概率;
(2)根据以上模拟试验的结果,将频率视为概率:
(ⅰ)若活动期间某单位购买四台电视,求恰好有两台获奖的概率;
(ⅱ)若本次活动平均每台电视的奖金不超过260元,求m的最大值.
函数 .
.
(1)求函数 的极值;
的极值;
(2)设函数 ,对
,对 ,都有
,都有 ,求实数m的取值范围.
,求实数m的取值范围.
已知a>0,且 .设命题
.设命题 :函数
:函数 在(0,+∞)上单调递减,命题
在(0,+∞)上单调递减,命题 :曲线
:曲线 与x轴交于不同的两点,如果
与x轴交于不同的两点,如果 是假命题,
是假命题, 是真命题,求a的取值范围.
是真命题,求a的取值范围.