如图,矩形ABCD中,|AB|=4,|BC|=2,E,F,M,N分别是矩形四条边的中点,G,H分别是线段ON,CN的中点.
(1)证明:直线EG与FH的交点L在椭圆W: 上;
上;
(2)设直线l: 与椭圆W:
与椭圆W: 有两个不同的交点P,Q,直线l与矩形ABCD有两个不同的交点S,T,求
有两个不同的交点P,Q,直线l与矩形ABCD有两个不同的交点S,T,求 的最大值及取得最大值时m的值.
的最大值及取得最大值时m的值.
如图,AB是圆O的直径,点C在圆O上,延长BC到D使BC=CD,过C作圆O的切线交AD于E.若AB=6,ED=2,求BC的值.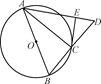
如图,PA切圆O于点A,割线PBC交圆O于点B、C,∠APC的角平分线分别与AB、AC相交于点D、E,求证:
(1)AD=AE;
(2)AD2=DB·EC.
如图,在△ABC中,∠B=90°,以AB为直径的圆O交AC于D,过点D作圆O的切线交BC于E,AE交圆O于点F.求证:
(1)E是BC的中点;
(2)AD·AC=AE·AF.
如图,圆O的直径AB=2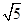 ,C是圆O外一点,AC交圆O于点E,BC交圆O于点D,已知AC=AB,BC=4,求△ADE的周长.
,C是圆O外一点,AC交圆O于点E,BC交圆O于点D,已知AC=AB,BC=4,求△ADE的周长.
如图,在△ABC中,已知CM是∠ACB的平分线,△AMC的外接圆交BC于点N.若AC= AB,求证:BN=2AM.
AB,求证:BN=2AM.