某家电专卖店在五一期间设计一项有奖促销活动,每购买一台电视,即可通过电脑产生一组3个数的随机数组,根据下表兑奖:
| 奖次 |
一等奖 |
二等奖 |
三等奖 |
| 随机数组的特征 |
3个1或3个0 |
只有2个1或2个0 |
只有1个1或1个0 |
| 资金(单位:元) |
5m |
2m |
m |
商家为了了解计划的可行性,估计奖金数,进行了随机模拟试验,并产生了20个随机数组,试验结果如下:
247,235,145,124,754,353,296,065,379,118,520,378,218,953,254,368,027,111,358,279.
(1)在以上模拟的20组数中,随机抽取3组数,至少有1组获奖的概率;
(2)根据以上模拟试验的结果,将频率视为概率:
(ⅰ)若活动期间某单位购买四台电视,求恰好有两台获奖的概率;
(ⅱ)若本次活动平均每台电视的奖金不超过260元,求m的最大值.
设函数
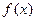 =cos(x+
=cos(x+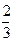 π)+cos
π)+cos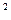
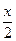 ,0<x<π
,0<x<π
(1)求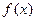 的值域;
的值域;
(2)设三角形ABC的内角A、B、C的对边分别为a、b、c,若f(B)=1,b=1,c=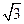 ,求边a的值
,求边a的值
已知数列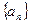 的前
的前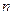 项和为
项和为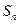 ,且
,且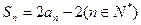 ,数列
,数列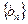 中,
中,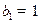 ,
,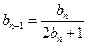 .(
.(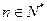 )
)
(1)求数列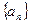 ,
,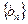 的通项
的通项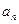 和
和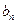
(2) 设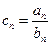 ,求数列
,求数列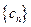 的前n项和
的前n项和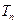 .
.
(3) 设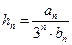 ,若对于一切
,若对于一切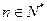 ,有
,有 恒成立,求
恒成立,求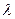 的取值范围
的取值范围
已知不等式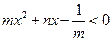 的解为
的解为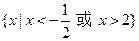
(1)求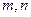 的值
的值
(2)解关于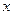 的不等式:
的不等式: 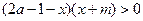 ,其中
,其中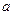 是实数
是实数
在△ABC中,a, b, c分别为内角A, B, C的对边,且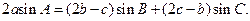
(1)求A的大小;
(2)求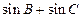 的最大值.
的最大值.
在等差数列{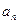 }中,
}中,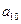 =18,前5项的和
=18,前5项的和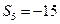
(1)求数列{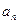 }的通项公式; (2)求数列{
}的通项公式; (2)求数列{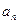 }的前
}的前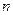 项和的最小值,并指出何时取最小.
项和的最小值,并指出何时取最小.