已知函数
(1) 若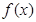 的一个极值点到直线
的一个极值点到直线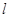 的距离为1,求
的距离为1,求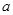 的值;
的值;
(2) 求方程 的根的个数.
的根的个数.
正方体.ABCD- 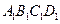 的棱长为l,点F为
的棱长为l,点F为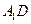 的中点.
的中点.
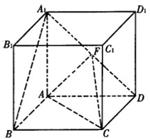
(I)(I)证明: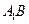 ∥平面AFC;.
∥平面AFC;.
(Ⅱ)求二面角B-AF-一-C的大小.







△ABC中,a,b,c分别是角A,B,C的对边,向量m=(2sinB,2-cos2B),
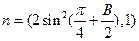 ,m⊥n,
,m⊥n,
(I)求角B的大小;
(Ⅱ)若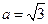 ,b=1,求c的值.
,b=1,求c的值.
已知函数f(x)=x2-4,设曲线y=f(x)在点(xn,f(xn))处的切线与x轴的交点为(xn+1,0)(n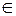
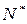 ),其中
),其中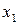 为正实数.
为正实数.
(Ⅰ)用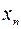 表示xn+1;
表示xn+1;
(Ⅱ)若a1=4,记an=lg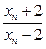 ,证明数列{
,证明数列{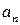 }成等比数列,并求数列{xn}的通项公式;
}成等比数列,并求数列{xn}的通项公式;
(Ⅲ)若x1=4,bn=xn-2,Tn是数列{bn}的前n项和,证明Tn<3.
用长为16米的篱笆,借助墙角围成一个矩形ABCD(如图),在P处有一棵树与两墙的距离分别为a米(0<a<12 )和4米。若此树不圈在矩形外,求矩形ABCD面积的最大值M.
已知函数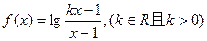 .
.
(1)求函数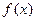 的定义域;
的定义域;
(2)若函数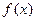 在[10,+∞)上单调递增,求k的取值范围.
在[10,+∞)上单调递增,求k的取值范围.