已知椭圆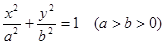 的离心率为
的离心率为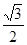 ,椭圆的左、右两个顶点分别为
,椭圆的左、右两个顶点分别为 ,
,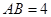 ,直线
,直线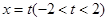 与椭圆相交于
与椭圆相交于 两点,经过三点
两点,经过三点 的圆与经过三点
的圆与经过三点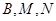 的圆分别记为圆C1与圆C2.
的圆分别记为圆C1与圆C2.
(1)求椭圆的方程;
(2)求证:无论 如何变化,圆C1与圆C2的圆心距是定值;
如何变化,圆C1与圆C2的圆心距是定值;
(3)当 变化时,求圆C1与圆C2的面积的和
变化时,求圆C1与圆C2的面积的和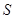 的最小值.
的最小值.
某小区要建一个面积为500平方米的矩形绿地,四周有小路,绿地长边外路宽5米,短边外路宽9米,怎样设计绿地的长与宽,使绿地和小路所占的总面积最小,并求出最小值。
成等差数列的三个数的和等于18,并且这三个数分别加上1,3, 17后就成了等比数列,求这三个数.
设数列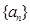 前
前 项和为
项和为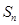 , 满足
, 满足  .
.
(1)求数列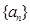 的通项公式;
的通项公式;
(2)令 求数列
求数列 的前
的前 项和
项和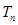 ;
;
(3)若不等式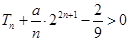 对任意的
对任意的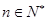 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
某兴趣小组测量电视塔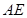 的高度
的高度 (单位
(单位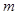 ),如示意图,垂直放置的标杆
),如示意图,垂直放置的标杆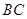 高度
高度 ,仰角
,仰角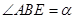 ,
, .
.
(1)该小组已经测得一组 的值,
的值,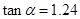 ,
,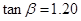 ,请据此算
,请据此算 的值;
的值;
(2)该小组分析若干测得的数据后,认为适当调整标杆到电视塔的距离 (单位
(单位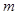 ),使
),使 与
与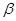 之差较大,可以提高测量精确度,若电视塔实际高度为
之差较大,可以提高测量精确度,若电视塔实际高度为 ,问
,问 为多少时,
为多少时, 最大?
最大?
已知集合 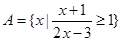 ,
, 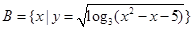 ,
,
求 .
.