某重点中学的高二英语老师Vivien,为调查学生的单词记忆时间开展问卷调查。发现在回收上来的1000份有效问卷中,有600名同学们背英语单词的时间安排在白天,另外400名学生晚上临睡前背。Vivien老师用分层抽样的方法抽取50名学生进行实验,实验方法是使两组学生记忆40个无意义音节(如XIQ、GEH),均要求在刚能全部记清时就停止识记,并在8小时后进行记忆测验。不同的是,甲组同学识记结束后一直不睡觉,8小时后测验;乙组同学识记停止后立刻睡觉,8小时后叫醒测验。
乙组同学识记停止8小时后的准确回忆(保持)情况如图。
(1)由分层抽样方法,抽取的50名学生乙组应有几名?
(2)从乙组准确回忆音节数在[8,20)范围内的学生中随机选2人,求两人均准确回忆12个(含12个)以上的概率;
(3)若从是否睡前记忆单词和单词小测能否优秀进行统计,运用2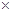 2列联表进行独立性检验,经计算K2=4.069,参考下表你能得到什么统计学结论?
2列联表进行独立性检验,经计算K2=4.069,参考下表你能得到什么统计学结论?
P(K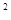 ≥k0) ≥k0) |
0.100 |
0.050 |
0.025 |
0.010 |
0.001 |