某电视台举办了“中华好声音”大型歌手选秀活动,过程分为初赛、复赛和决赛,经初赛进入复赛的40名选手被平均分成甲、乙两个班,由组委会聘请两位导师各负责一个班进行声乐培训。下面是根据这40名选手参加复赛时获得的100名大众评审的支持票数制成的茎叶图:
赛制规定:参加复赛的40名选手中,获得的支持票数排在前5名的选手可进入决赛,若第5名出现并列,则一起进入决赛;另外,票数不低于95票的选手在决赛时拥有“优先挑战权”。
1、从进入决赛的选手中随机抽出3名,求其中恰有1名拥有“优先挑战权”的概率;
2、电视台决定,复赛票数不低于85票的选手将成为电视台的“签约歌手”,请填写下面的2×2列联表,并判断“能否在犯错误的概率不超过0.025的前提下认为成为‘签约歌手’与选择的导师有关?
| |
甲班 |
乙班 |
合计 |
| 签约歌手 |
|
|
|
| 末签约歌手 |
|
|
|
| 合计 |
|
|
|
下面临界值表仅供参考:
| P(K2≥k) |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
| k |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
参考公式:K2= ,其中
,其中
(满分12分)一台机器使用的时间较长,但还可以使用,它按不同的转速生产出来的某机械零件有一些会有缺点,每小时生产有缺点零件的多少,随机器运转的速度而变化,下表为抽样试验的结果:
| 转速x(转/秒) |
16 |
14 |
12 |
8 |
| 每小时生产有缺点的零件数y(件) |
11 |
9 |
8 |
5 |
(Ⅰ)画出散点图;
(Ⅱ)如果y对x有线性相关关系,求回归直线方程;
(Ⅲ)若实际生产中,允许每小时的产品中有缺点的零件最多为10个,那么机器的运转速度应控制在什么范围内?
参考公式:
(满分12分)观察下列式子: ,
, ,
, ,
,
(Ⅰ)由此猜想一个一般性的结论,
(Ⅱ)请证明你的结论。
(满分12分)学习雷锋精神前半年内某单位餐厅的固定餐椅经常有损坏,学习雷锋精神时全修好;单位对学习雷锋精神前后各半年内餐椅的损坏情况作了一个大致统计,具体数据如下:
| 损坏餐椅数 |
未损坏餐椅数 |
总 计 |
|
| 学习雷锋精神前 |
50 |
150 |
200 |
| 学习雷锋精神后 |
30 |
170 |
200 |
| 总计 |
80 |
320 |
400 |
(Ⅰ)求:学习雷锋精神前后餐椅损坏的百分比分别是多少?并初步判断损毁餐椅数量与学习雷锋精神是否有关?
(Ⅱ)请说明是否有97.5%以上的把握认为损毁餐椅数量与学习雷锋精神有关?
参考公式: ,
,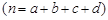
| P(K2≥k0) |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
| k0 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
(满分12分)复数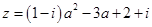 (
(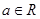 ),
),
(Ⅰ)若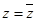 ,求
,求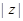 ;
;
(Ⅱ)若在复平面内复数 对应的点在第一象限,求
对应的点在第一象限,求 的范围.
的范围.
已知函数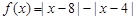 .
.
(Ⅰ)作出函数y = f(x)的图像:
(Ⅱ)解不等式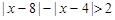 .
.