（满分12分）一台机器使用的时间较长，但还可以使用，它按不同的转速生产出来的某机械零件有一些会有缺点，每小时生产有缺点零件的多少，随机器运转的速度而变化，下表为抽样试验的结果：
| 转速x（转/秒） |
16 |
14 |
12 |
8 |
| 每小时生产有缺点的零件数y（件） |
11 |
9 |
8 |
5 |
（Ⅰ）画出散点图；
（Ⅱ）如果y对x有线性相关关系，求回归直线方程；
（Ⅲ）若实际生产中，允许每小时的产品中有缺点的零件最多为10个，那么机器的运转速度应控制在什么范围内？
参考公式：
本小题满分12分）
甲、乙两位学生参加数学竞赛培训.现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次，记录如下：
甲 82 81 79 78 95 88 93 84
乙 92 95 80 75 83 80 90 85
（Ⅰ）用茎叶图表示这两组数据；
（Ⅱ）现要从中选派一人参加数学竞赛，你认为选派哪位学生参加合适？请说明理由.
对于定义域分别为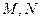
的函数
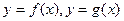，规定：
函数
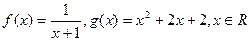(1)若函数
,求函数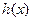
的取值集合；
(2)若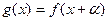
，其中
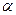是常数，且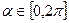
，请问，是否存在一个定义域为
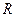的函数
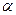及一个的值，使得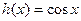
，若存在请写出一个
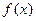的解析式及一个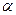的值，若不存在请说明理由。
已知椭圆C的左，右焦点坐标分别为
,离心率是
。椭圆C的左，右顶点分别记为A,B。点S是椭圆C上位于
轴上方的动点，直线AS,BS与直线
分别交于M,N两点。
（1）求椭圆C的方程；
（2）求线段MN长度的最小值；
（3）当线段MN的长度最小时，在椭圆C上的T满足：T到直线AS的距离等于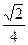
.
试确定点T的个数。
设函数
，其图像过点（0,1）.
（1）当方程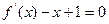
的两个根分别为是
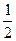，1时,求f(x)的解析式；
（2）当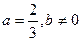
时，求函数f(x)的极大值与极小值.
已知三棱锥P-ABC中，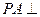
平面ABC, 
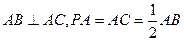,N为AB上一点，AB=" 4AN," M ,D ,S分别为PB,AB,BC的中点。
（1）求证： PA//平面CDM;
（2）求证： SN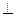
平面CDM.