如图（a）为一研究电磁感应的实验装置示意图，其中电流传感器（相当于一只理想的电流表）能将各时刻的电流数据实时通过数据采集器传输给计算机，经计算机处理后在屏幕上同步显示出
图像。足够长光滑金属轨道电阻不计，倾角θ=30°。轨道上端连接有阻值R=1.0Ω的定值电阻，金属杆MN电阻r=0.5Ω，质量m=0.2kg，杆长
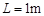。在轨道区域加一垂直轨道平面向下的匀强磁场，让金属杆从图示位置由静止开始释放，此后计算机屏幕上显示出如图（b）所示的图像（设杆在整个运动过程中与轨道垂直，
）。试求：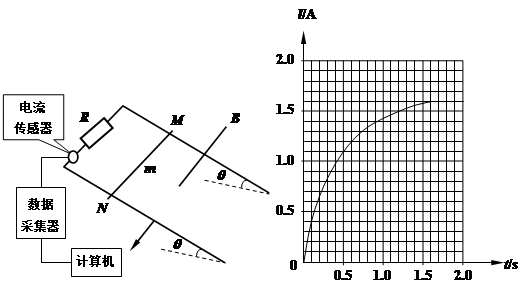
图（a） 图（b）
（1）t=0.5s时电阻R的热功率；
（2）匀强磁场的磁感应强度B的大小；
（3）估算0~1.2s内通过电阻R的电量大小及在R上产生的焦耳热。
半人马星座α星是太阳系最近的恒星，它距地球为4.3×1016 m.设有一宇宙飞船自地球往返于半人马星座α星之间.若宇宙飞船的速度为0.999c，按地球上的时钟计算，飞船往返一次需多长时间？如以飞船上的时钟计算，往返一次的时间又为多长？
2003年10月15日，我国用“长征”二号F运载火箭成功地将“神舟”五号载人飞船送入预定轨道（距离地面高度约340 km），飞船绕地球飞行14圈后，约用时21小时，于16日6时23分成功返回地球．我国首位造访太空的飞行员杨利伟自主出舱．这标志着我国已经成为世界上第三个独立自主地完整掌握载人航天、有能力将人送入太空的国家，这再次证明中国有能力攀登世界科技高峰，自立于世界民族之林．
（1）“神舟”五号飞船的轨道半径是多少？其运行速度多大？（地球质量为6.0×1024 kg，地球半径为6.4×106 m）
（2）飞船在竖直向上发射升空阶段、进入轨道绕地球做匀速圆周运动阶段和返回地球竖直向下加速下降阶段，杨利伟分别处于什么状态（）
| A．超重，完全失重，失重 | B．超重，完全失重，超重 |
| C．超重，失重，完全失重 | D．失重，完全失重，超重 |
金星的半径是地球的0.95倍，质量为地球的0.82倍，金星表面的自由落体加速度是多大？金星的第一宇宙速度是多大？
“2003年10月15日9时，我国神舟五号宇宙飞船在洒泉卫星发射中心成功发射，把中国第一位航天员杨利伟送入太空。飞船绕地球飞行14圈后，于10月16日6时23分安全降落在蒙古主着陆场。”根据以上消息，近似地把飞船从发射到降落的全部运动看做绕地球的匀速圆周运动，试估算神舟五号绕地球飞行时距地面的高度（已知地球的质量为M=6.0×1024kg，地球的半径R=6.4×103km）。
利用所学知识，推导第一宇宙速度的另一表达式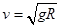
。