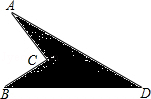
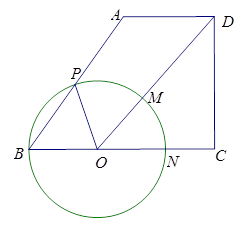
如图,在梯形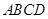 中
中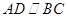 ,
,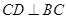 ,已知
,已知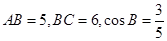 ,点
,点 为
为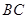 边上的动点,连接
边上的动点,连接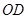 ,以
,以 为圆心,
为圆心, 为半径的⊙
为半径的⊙ 分别交射线
分别交射线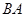 于点
于点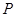 ,交射线
,交射线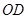 于点
于点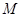 ,交射线
,交射线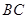 于
于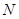 ,连接
,连接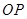 .
.
(1)求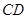 的长.
的长.
(2)当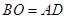 时,求
时,求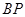 的长.
的长.
(3)在点 的运动过程中,
的运动过程中,
①当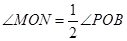 时,求⊙
时,求⊙ 的半径.
的半径.
②当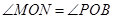 时,求⊙
时,求⊙ 的半径(直接写出答案).
的半径(直接写出答案).
化简:
(1)
(2)解不等式组 ;并求它的最小整数解.
;并求它的最小整数解.
如图,直线OC、BC的函数关系式分别是y1=x和y2=﹣2x+6,动点P(x,0)在OB上运动(0<x<3),过点P作直线m与x轴垂直.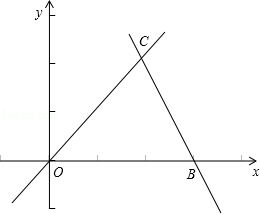
(1)求点C的坐标,并回答当x取何值时y1>y2?
(2)设△COB中位于直线m左侧部分的面积为s,求出s与x之间函数关系式.
(3)当x为何值时,直线m平分△COB的面积?
如图,平行四边形ABCD的对角线AC,BD交于点0,E,F在AC上,G,H在BD上,且AF=CE,BH=DG.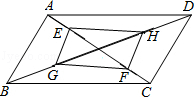
求证:FG∥HE.
已知一次函数的图象过点(3,5)与点(﹣4,﹣9),求这个一次函数的解析式.
如图,已知AC=4,BC=3,BD=12,AD=13,∠ACB=90°,试求阴影部分的面积.