（1）操作发现：如图①，D是等边△ABC边BA上一动点（点D与点B不重合），连接DC，以DC为边在BC上方作等边△DCF，连接AF．你能发现线段AF与BD之间的数量关系吗？并证明你发现的结论．
（2）类比猜想：如图②，当动点D运动至等边△ABC边BA的延长线上时，其他作法与（1）相同，猜想AF与BD在（1）中的结论是否仍然成立？
（3）深入探究：
Ⅰ．如图③，当动点D在等边△ABC边BA上运动时（点D与点B不重合）连接DC，以DC为边在BC上方、下方分别作等边△DCF和等边△DCF′，连接AF、BF′，探究AF、BF′与AB有何数量关系？并证明你探究的结论．
Ⅱ．如图④，当动点D在等边△边BA的延长线上运动时，其他作法与图③相同，Ⅰ中的结论是否成立？若不成立，是否有新的结论？并证明你得出的结论．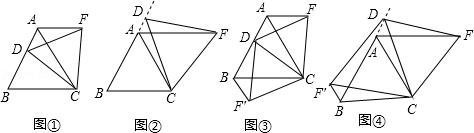
一辆货车从超市出发，向东走3千米到达小李家，继续向东走1.5千米到达小张家，然后又回头向西走9.5千米到达小陈家，最后回到超市。
（1）以超市为原点，向东为正，以1个单位长表示1千米，在数轴上表示出上述位置。
（2）小陈家距小李家多远？
（3）若货车每千米耗油0. 5升，这趟路货车共耗油多少升？
有
筐白菜，以每筐
千克为标准，超过的千克数记作正数，不足的千克数记作负数，称后的纪录如下：
回答下列问题：
（1）这筐白菜中最接近标准重量的这筐白菜重千克；
（2）这筐白菜一共重多少千克？
课堂上王老师给大家出了这样一道题，“当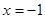
时，求代数式
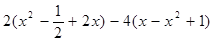的值”，小明一看，“太复杂了，怎么算呢？”你能帮小明解决这个问
题吗？请写出具体过程。
化简求值：
，其中
≥
的负整数解。