为纪念“光纤之父”、诺贝尔物理学奖获得者高锟的杰出贡献,早在1996年中国科学院紫金山天 文台就将一颗于1981年12月3日发现的国际编号为“3463”的小行星命名为“高锟星”。已知“高锟星”半径为R,其表面的重力加速度为g,万有引力常量为G,在不考虑自转的情况,求解以下问题:(以下结果均用字母表达即可)
(1)假设“高锟星”为一均匀球体,试求“高锟星”的平均密度;(球体积 )
)
(2)卫星环绕“高锟星”运行的第一宇宙速度;
(3)假设某卫星绕“高锟星”做匀速圆周运动且运行周期为T,求该卫星距地面的高度。
如图所示,质量M=2√3kg的木块A套在水平杆上,并用轻绳将木块:A与质量m=√3kg的小球相连。今用跟水平方向成α=30°角的力F=10√3N,拉着球带动木块一起向右匀速运动,运动中M、m相对位置不变,取g=10m/s2。求: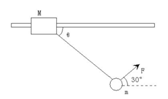
(1)运动过程中轻绳与水平方向夹角θ。
(2)木块与水平杆间的动摩擦因数为μ。
所受重力G1=8N的砝码悬挂在绳PA和PB的结点上,PA偏离竖直方向37°角,PB在水平方向,且连在所受重力为G2=100N的木块上,木块静止于倾角为37°的斜面上,如图所示,试求:
(1)木块与斜面间的摩擦力?
(2)木块所受斜面的弹力?
汽车从静止开始以2m/s2的加速度前进,同时,某人从车后相距s0=20m处开始以8m/s的速度匀速追车。讨论:人能否追上前面的汽车?若追不上,求人车之间的最小距离;若追得上,求追上所用的时间.
质点从静止开始做匀加速直线运动,经4s后速度达到20m/s,然后匀速运动了10s,接着经5s匀减速运动后静止。求:
(1)质点在加速运动阶段和减速阶段的加速度的大小?
(2)质点在整个过程的平均速度是多大?
一物体向北做匀变速直线运动,经0.2 s时间速度由12 m/s减少到8 m/s,求:(1)该物体的加速度大小为多少m/s2?加速度的方向?(2)这段时间的位移是多少m?位移的方向?