下图是一个按照某种规律排列出来的三角形数阵
假设第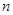 行的第二个数为
行的第二个数为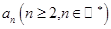
(1)依次写出第七行的所有7个数字(不必说明理由);
(2)写出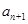 与
与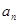 的递推关系(不必证明),并求出
的递推关系(不必证明),并求出 的通项公式
的通项公式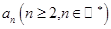 .
.
如图,在正方体ABCD-A1B1C1D1中,E、F为棱AD、AB的中点.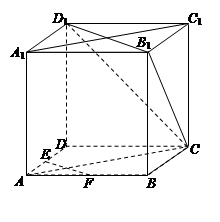
(1)求证:EF∥平面CB1D1;
(2)求证:平面CAA1C1⊥平面CB1D1.
在平面直角坐标系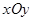 中,已知点A(-2,1),直线
中,已知点A(-2,1),直线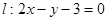 。
。
(1)若直线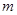 过点A,且与直线
过点A,且与直线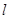 垂直,求直线
垂直,求直线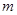 的方程;
的方程;
(2)若直线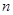 与直线
与直线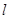 平行,且在
平行,且在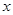 轴、
轴、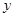 轴上的截距之和为3,求直线
轴上的截距之和为3,求直线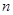 的方程。
的方程。
已知函数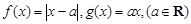 .
.
(1)判断函数 的奇偶性;
的奇偶性;
(2)若关于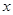 的方程
的方程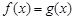 有两解,求实数
有两解,求实数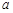 的取值范围;
的取值范围;
(3)若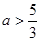 ,记
,记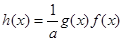 ,试求函数
,试求函数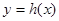 在区间
在区间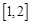 上的最大值.
上的最大值.
(本小题满分16分)
已知函数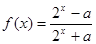 ,若
,若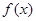 为定义在R上的奇函数,则(1)求实数
为定义在R上的奇函数,则(1)求实数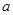 的值;(2)求函数
的值;(2)求函数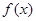 的值域;(3)求证:
的值域;(3)求证: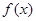 在R上为增函数;(4)若m为实数,解关于
在R上为增函数;(4)若m为实数,解关于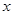 的不等式:
的不等式: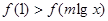
(本小题满分16分)
已知函数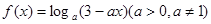 (1)求函数
(1)求函数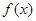 的定义域;
的定义域;
(2)若函数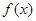 在[2,6]上递增,并且最小值为
在[2,6]上递增,并且最小值为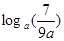 ,求实数
,求实数 的值。
的值。