如图所示,质量为M的长方形木板静止在光滑水平面上,木板的左侧固定一劲度系数为k的轻质弹簧,木板的右侧用一根伸直的并且不可伸长的轻绳水平地连接在竖直墙上。 绳所能承受的最大拉力为T0一质量为m的小滑块以一定的速度在木板上无摩擦地向左运动,而后压缩弹簧。弹簧被压缩后所获得的弹性势能可用公式 计算,k为劲度系数,z为弹簧的形变量。
计算,k为劲度系数,z为弹簧的形变量。

(1)若在小滑块压缩弹簧过程中轻绳始终未断,并且弹簧的形变量最大时,弹簧对木板 的弹力大小恰好为T,求此情况下小滑块压缩弹簧前的速度v0;
(2)若小滑块压缩弹簧前的速度 为已知量,并且大于(1)中所求的速度值
为已知量,并且大于(1)中所求的速度值 求此情况下弹簧压缩量最大时,小滑块的速度;
求此情况下弹簧压缩量最大时,小滑块的速度;
(3)若小滑块压缩弹簧前的速度人于(1)中所求的速度值v0,求小滑块最后离开木板时,相对地面速度为零的条件。
如图所示,水平地面上叠放着物块A和木板B,物块A用水平轻质弹簧拉着固定在墙上。已知,物体A的质量mA=5kg,木板B的质量mB=10kg,物块与木板之间、木板与地面之间的动摩擦因数均为μ=0.2,弹簧的劲度系数k=200N/m。g 取10 N/kg,若要将物木板B从A的下方匀速拉出。求: 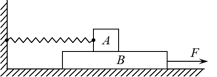
(1)轻质弹簧的伸长量x;
(2)作用在物块B上的水平拉力F的大小。
水平放置的平行金属板AB间的距离d=0.1m,板长L=0.3m,在金属板的左端竖直放置一带有小孔的挡板,小孔恰好位于AB板的正中间,距金属板右端x=0.5m处竖直放置一足够大的荧光屏,现在AB板间加如图(b)所示的方波形电压,已知U0=1.0×102V,在挡板的左侧,有大量带正电的相同粒子以平行于金属板方向的速度持续射向挡板,粒子的质量m=1.0×10-7kg,电荷量q=1.0×10-2C,速度大小均为v0=1.0×104m/s,带电粒子的重力不计,则: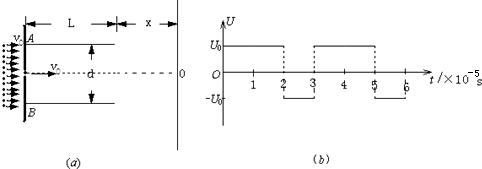
(1)求粒子在电场中的运动时间;
(2)求在t=0时刻进入的粒子打在荧光屏上的位置到O点的距离;
(3)请证明粒子离开电场时的速度均相同;
(4)若撤去挡板,求荧光屏上出现的光带长度。
如图所示,A为电解槽(电能转化为化学能的装置),M为电动机,N为电炉子,恒定电压U=12V,电解槽内阻rA=2Ω,当K1闭合,K2、K3断开时,电流表示数I1=6A;当K2闭合,K1、K3断开时,电流表示数I2=3A,且电动机输出功率为13.5W;当K3闭合,K1、K2断开时,电流表示数为I3=2A.不计电流表内阻,求:
(1)电炉子的电阻R及发热功率PR;
(2)电动机的内阻rM;
(3)在电解槽工作时,电能转化为化学能的功率P化。
从电子枪射出初速度不计的电子束,如图所示,经电压U1=180V的加速电场加速后,从正中间平行进入金属板Y和Y′,电子束穿过两板后最终垂直打在荧光屏上的O点.若现在用一输出电压为U2=160V的稳压电源与金属板YY′连接,在YY′间产生匀强电场,使得电子束发生偏转.若取电子质量为m=9×10﹣31kg,带电量e=1.60×10﹣19C,YY′两板间距d=9.0cm,板长l=9.0cm,板的末端到荧光屏的距离L=13.5cm.整个装置处于真空中,不考虑重力的影响,试回答以下问题:
(1)电子束射入金属板YY′时速度v0;
(2)加上电压U2后电子束打到荧光屏上的位置到O点的距离y′;
(3)如果两金属板YY′间的距离d可以随意调节(保证电子束仍从两板正中间射入),其他条件都不变,试求电子束打到荧光屏上的位置到O点距离的取值范围.
如图示电路中,电阻R1=R2=6Ω,R3=4Ω,R4=3Ω。电源内阻r=2Ω。不计电压表和电流表的影响。S断开时,电压表的示数为2.25V。求: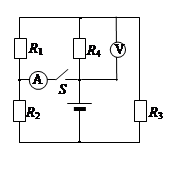
(1)电源电动势E;
(2)S合上后,电流表的示数。