水平放置的平行金属板AB间的距离d=0.1m,板长L=0.3m,在金属板的左端竖直放置一带有小孔的挡板,小孔恰好位于AB板的正中间,距金属板右端x=0.5m处竖直放置一足够大的荧光屏,现在AB板间加如图(b)所示的方波形电压,已知U0=1.0×102V,在挡板的左侧,有大量带正电的相同粒子以平行于金属板方向的速度持续射向挡板,粒子的质量m=1.0×10-7kg,电荷量q=1.0×10-2C,速度大小均为v0=1.0×104m/s,带电粒子的重力不计,则: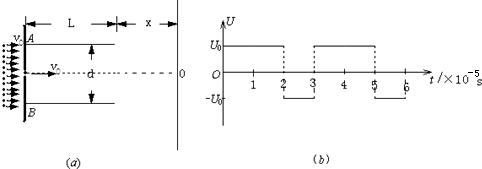
(1)求粒子在电场中的运动时间;
(2)求在t=0时刻进入的粒子打在荧光屏上的位置到O点的距离;
(3)请证明粒子离开电场时的速度均相同;
(4)若撤去挡板,求荧光屏上出现的光带长度。
有一种大型游戏机叫“跳楼机”(如图所示),参加游戏的游客被安全带固定在座椅上,由电动机将座椅沿光滑的竖直轨道提升到离地面40 m高处,然后由静止释放.可以认为座椅沿轨道做自由落体运动2 s后,开始受到恒定阻力而立即做匀减速运动,且下落到离地面4 m高处时速度刚好减小到零。然后再让座椅以相当缓慢的速度稳稳下落,将游客送回地面.取g=10 m/s2,求:
(1)座椅在自由下落结束时刻的速度是多大?
(2)座椅在匀减速阶段的时间是多少?
(3)在匀减速阶段,座椅对游客的作用力大小是游客体重的多少倍?
如图所示,在斜面上放着一个重为100N的物体,斜面倾角为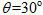 时物体恰能沿斜面匀速下滑,求
时物体恰能沿斜面匀速下滑,求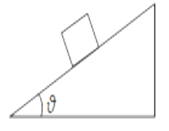
(1)物体和斜面的动摩擦因数
(2)当斜面倾角为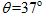 时,让物体沿斜面下滑,在下滑过程中物体受到的摩擦力多大?(
时,让物体沿斜面下滑,在下滑过程中物体受到的摩擦力多大?(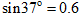 ,
,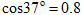 )
)
如图所示,在光滑的水平面上放置一个质量为2m的木板B,B的左端放置一个质量为m的物块A,已知A、B之间的动摩擦因数为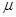 ,现有质量为m的小球以水平速度
,现有质量为m的小球以水平速度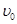 飞来与A物块碰撞后立即粘住,在整个运动过程中物块A始终未滑离木板B,且物块A和小球均可视为质点(重力加速度g)。求:
飞来与A物块碰撞后立即粘住,在整个运动过程中物块A始终未滑离木板B,且物块A和小球均可视为质点(重力加速度g)。求: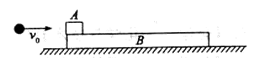
①物块A相对B静止后的速度大小;
②木板B至少多长。
如图所示,将一等腰直角棱镜ABC截去棱角ADE,使其截面DE平行于底面BC,可制成“道威棱镜”,这样就减小了棱镜的重量和杂散的内部反射。已知棱镜玻璃的折射率n= ,棱边长
,棱边长 cm,
cm, cm,一束平行于底边BC的单色光从DE边上的M点射入棱镜,求:
cm,一束平行于底边BC的单色光从DE边上的M点射入棱镜,求:
(i)光线进入“道威棱镜”时的折射角;
(ii)通过计算判断光线能否从BC边射出;
(ⅲ)光线在棱镜中传播所用的时间。
如图所示,两端开口、粗细均匀的长直U形玻璃管内由两段水银柱封闭着长度为15cm的空气柱,气体温度为300K时,空气柱在U形管的左侧。
(i)若保持气体的温度不变,从左侧开口处缓慢地注入25cm长的水银柱,管内的空气柱长为多少?
(ii)为了使空气柱的长度恢复到15cm,且回到原位置,可以向U形管内再注入一些水银,并改变气体的温度,应从哪一侧注入长度为多少的水银柱?气体的温度变为多少?
(大气压强P0=75cmHg,图中标注的长度单位均为cm)