已知数列{an}为等差数列，Sn为其前n项和，且
，
．
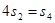（1）求数列{an}的通项公式；
（2）求证数列
是等比数列；
（3）求使得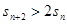
的成立的n的集合．
已知
各项均为正数的数列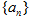
满足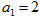
，
，
．
（1）求证：数列
是等比数列；
（2）当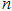
取何值时，
取最大值，并求出最大值；
（3）若
对任意
恒成立，求实数
的取值范围．
已知椭圆C：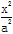
＋
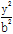＝1（a＞b＞0）的离心率为
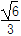，短轴一个端点到右焦点的距离为
．
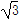（1）求椭圆C的方程；
（2）设直线l与椭圆C交于A、B两点，坐标原点O到直线l的距离为
，求△AOB面积的最大值．
某运输公司有12名驾驶员和19名工人，有8辆载重量为10t的甲型卡车和7辆载重量为6t的乙型卡车，某天需送往A地至少72t的货物，派用的每辆车需载满且只运送一次，派用的每辆甲型卡车需配2名工人，运送一次可得利润450元；派用的每辆乙型卡车需配1名工人；运送一次可得利润350元，该公司合理计划当天派用甲乙卡车的车辆数，求公司最大利润．
已知函数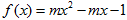
．
（1）若对于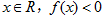
恒成立，求实数
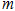的取值范围；
（2）若对于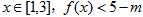
恒成立，求实数
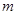的取值范围．
命题p：实数x满足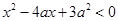
，其中a＜0，命题q：实数x满足
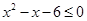或
，且
的必要不充分条件，求a的取值范围．