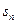已知二次函数 .
.
(1)若 ,试判断函数
,试判断函数 零点个数;
零点个数;
(2)是否存在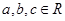 ,使
,使 同时满足以下条件
同时满足以下条件
①对任意 ,且
,且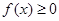 ;
;
②对任意 ,都有
,都有 。若存在,求出
。若存在,求出 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。
(3)若对任意 且
且 ,
, ,试证明存在
,试证明存在 ,
,
使 成立。
成立。
(本小题满分14分)某公司计划2010年在甲、乙两个电视台做总时间不超过300分钟的广告,广告总费用不超过9万元,甲、乙电视台的广告收费标准分别为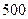 元/分钟和200元/分钟,规定甲、乙两个电视台为该公司所做的每分钟广告,能给公司事来的收益分别为0.3万元和0.2万元.问该公司如何分配在甲、乙两个电视台的广告时间,才能使公司的收益最大,最大收益是多少万元?
元/分钟和200元/分钟,规定甲、乙两个电视台为该公司所做的每分钟广告,能给公司事来的收益分别为0.3万元和0.2万元.问该公司如何分配在甲、乙两个电视台的广告时间,才能使公司的收益最大,最大收益是多少万元?
(本小题满分16分)已知数列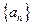 :
:
①观察规律,归纳并计算数列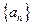 的通项公式,它是个什么数列?
的通项公式,它是个什么数列?
②若 ,设
,设 =
= ,求
,求 。
。
③设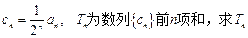
(本小题满分16分)已知关于x的二次方程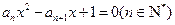 的两根
的两根 满足
满足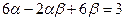 ,且
,且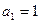
(1)试用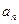 表示
表示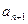 ;(2)求证:数列
;(2)求证:数列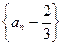 是等比数列;
是等比数列;
(3)求数列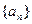 的前n项和
的前n项和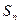 .
.
(本小题满分12分)数列 的前
的前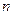 项和为
项和为 ,
,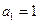 ,
, .求数列
.求数列 的通项
的通项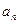
(本小题满分12分)等比数列{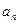 }的前n 项和为
}的前n 项和为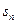 ,已知
,已知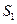 ,
, ,
,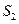 成等差数列
成等差数列
(1)求{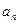 }的公比q;
}的公比q;
(2)求 -
-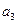 =3,求
=3,求