(本小题满分12分)等比数列{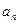 }的前n 项和为
}的前n 项和为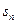 ,已知
,已知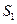 ,
, ,
,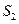 成等差数列
成等差数列
(1)求{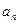 }的公比q;
}的公比q;
(2)求 -
-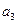 =3,求
=3,求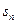


(本小题满分12分)在四棱柱 中,
中, ,底面
,底面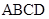 为菱形,
为菱形,
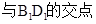 ,已知
,已知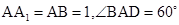 .
.
(1)求证:平面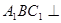 平面
平面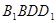 ;
;
(2)求点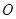 到平面
到平面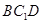 的距离.
的距离.
(本小题满分12分)设向量 ,其中
,其中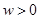 ,
, ,已知函数
,已知函数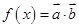 的最小正周期为
的最小正周期为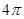 .
.
(1)求 的对称中心;
的对称中心;
(2)若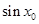 是关于
是关于 的方程
的方程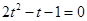 的根,且
的根,且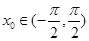 ,求
,求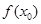 的值.
的值.
(本小题满分10分)已知集合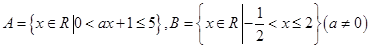 .
.
(1)若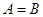 ,求出实数
,求出实数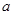 的值;
的值;
(2)若命题 命题
命题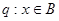 且
且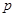 是
是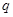 的充分不必要条件,求实数
的充分不必要条件,求实数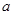 的取值范围.
的取值范围.
(本小题满分12分)已知二次函数 对任意实数
对任意实数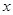 都满足
都满足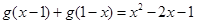 ,且
,且 .令
.令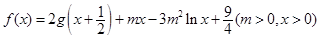 .
.
(1)若函数 在
在 上的最小值为0,求
上的最小值为0,求 的值;
的值;
(2)记函数 ,若函数
,若函数 有5个不同的零点,求实数
有5个不同的零点,求实数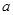 的取值范围.
的取值范围.
(本小题满分12分)在直角坐标 平面内,已知点
平面内,已知点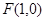 ,直线
,直线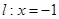 ,
, 为平面上的动点,过
为平面上的动点,过 作直线
作直线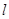 的垂线,垂足为点
的垂线,垂足为点 ,且
,且 .
.
(1)求动点 的轨迹
的轨迹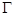 的方程;
的方程;
(2)过点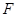 的直线交轨迹
的直线交轨迹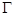 于
于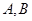 两点,交直线
两点,交直线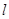 于点
于点 ,已知
,已知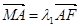 ,
,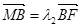 ,,试判断
,,试判断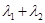 是否为定值,若是,求出该定值;若不是,请说明理由.
是否为定值,若是,求出该定值;若不是,请说明理由.