把函数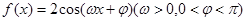 的图像上每一点的横坐标伸长到原来的2倍,纵坐标不变,然后再向左平移
的图像上每一点的横坐标伸长到原来的2倍,纵坐标不变,然后再向左平移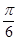 个单位后得到一个最小正周期为2
个单位后得到一个最小正周期为2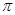 的奇函数
的奇函数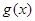 .
.
(1) 求 的值;
的值;
(2)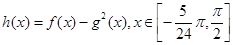 的单调区间和最值.
的单调区间和最值.
(本小题满分14分)某实验室某一天的温度(单位: )随时间t(单位:h)的变化近似满足函数关系:
)随时间t(单位:h)的变化近似满足函数关系: ,
, .
.
(1)求实验室这一天里,温度降低的时间段;
(2)若要求实验室温度不高于10 ,则在哪段时间实验室需要降温?
,则在哪段时间实验室需要降温?
已知函数 .
.
(1)求函数 单调区间;
单调区间;
(2)若在区间 上,
上, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(本小题满分14分)在 中,内角
中,内角 ,
, ,
, 的对边分别为
的对边分别为 ,
, ,
, ,且
,且 .
.
(1)求角 的大小;
的大小;
(2)若 ,
, ,求
,求 的面积.
的面积.
(本小题满分14分)已知函数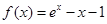 ,
, , 其中,
, 其中,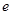 是自然对数的底数.函数
是自然对数的底数.函数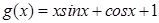 ,
,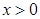 .
.
(Ⅰ)求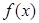 的最小值;
的最小值;
(Ⅱ)将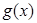 的全部零点按照从小到大的顺序排成数列
的全部零点按照从小到大的顺序排成数列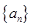 ,求证:
,求证:
(1)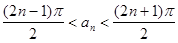 ,其中
,其中 ;
;
(2)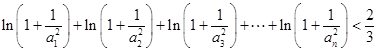 .
.
(本小题满分13分)如图,已知抛物线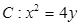 ,过焦点F任作一条直线与
,过焦点F任作一条直线与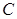 相交于
相交于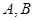 两点,过点
两点,过点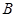 作
作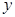 轴的平行线与直线
轴的平行线与直线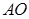 相交于点
相交于点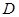 (
( 为坐标原点).
为坐标原点).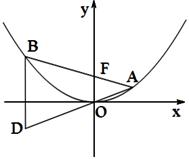
(Ⅰ)证明:动点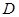 在定直线上;
在定直线上;
(Ⅱ)点P为抛物线C上的动点,直线 为抛物线C在P点处的切线,求点Q(0,4)到直线
为抛物线C在P点处的切线,求点Q(0,4)到直线 距离的最小值.
距离的最小值.